Chapter 12 Tables of counts
12.1 Introduction
Sometimes our data are summarised as tables of counts (or contingency tables); this might be a frequency distribution if there is only one variable (one-way table) or as a cross-tabulation if there are two discrete variables (two-way table). We can still ask questions of these data to test hypotheses and the general approach is similar to that previously described but the reference distribution used is a \(\chi^2\) (pronounced ‘chi-square’) distribution.
Chi-square tests on contingency tables look at the distributions of counts over the cells (in the table) and we ask does a particular row or column distribution differ significantly from some other distribution. We consider two different types of test; a goodness-of-fit test used on a one-way table and a test of independence used on a cross-tabulation. As usual, the validity of conclusions based on these tests rely on some assumptions being met and these are described.
12.2 \(\chi^2\) goodness-of-fit test
As a motivating example, we consider data collected from the Scottish Schools Adolescent Lifestyle and Substance Use Survey (SALSUS) established by the Scottish Executive to monitor substance use among young people in Scotland. School pupils in independent and local authority schools were targeted and the data we use are from 2002 - the total sample size was 22,246 pupils.
Pupils were asked to record the ethnic group to which they identified, (note that the groups were then combined into five broad categories); the numbers in each group are shown in Table 12.1.
| Group | Frequency |
|---|---|
| White | 21249 |
| Asian | 408 |
| Black | 113 |
| Mixed | 204 |
| Other | 272 |
| Total | 22246 |
We want to assess the similarity of the ethnicity recorded in the SALSUS sample to that of the population in Scotland. Table 12.2 shows the proportions of the ethnic groups recorded in the census.
| Group | Proportion |
|---|---|
| White | 0.9726 |
| Asian | 0.018 |
| Black | 0.0014 |
| Mixed | 0.005 |
| Other | 0.003 |
As for all tests, we have a null (\(H_0\)) and alternative hypothesis (\(H_1\)). In this case we want to test:
\[H_0: \textrm{the ethnicity in the sample is the same as the ethnicity in the population}\]
\[H_1: \textrm{the ethnicity in the sample is not the same as the ethnicity in the population}\]
The first step is to calculate what frequencies we would expect to see if the sample reflected the census population. These expected frequencies for each group (or cell in the table) can be obtained by:
\[\textrm{Expected value} = \textrm{total sample size} \times \textrm{expected cell proportion}\] Thus, for the ‘white’ group, the expected value is
\[ \textrm{Expected value} = 22246 \times 0.9726 = 21636.46\]
These expected values can be obtained for all groups (Table 12.3).
| Group | Frequency | Expected |
|---|---|---|
| White | 21249 | 21636 |
| Asian | 408 | 400.4 |
| Black | 113 | 31.14 |
| Mixed | 204 | 111.2 |
| Other | 272 | 66.74 |
To determine whether the sample data are consistent with the null hypothesis, we calculate a measure of difference between the observed and expected counts using the chi-square test statistic:
\[\chi_{stat}^2 = \sum_{\textrm{all cells}} \frac{(\textrm{observed count} - \textrm{expected count})^2}{\textrm{expected count}}\] This formula is frequently abbreviated to:
\[\chi_{stat}^2 = \sum_{\textrm{all cells}} \frac{(\textrm{O} - \textrm{E})^2}{\textrm{E}}\]
A key component to this statistic is a simple (squared) distance between what is predicted by our theory (in this case the census), and what we observed in our sample (i.e. O-E in the formula). The chi-square component for the White group is:
\[\chi_{white}^2 = \frac{(21249 - 21636.46)^2}{21636.46}= 6.938\]
The \(\chi^2\) contributions are calculated for all ethnic groups (Table 12.4).
| Group | Frequency | Expected | Chi |
|---|---|---|---|
| White | 21249 | 21636 | 6.939 |
| Asian | 408 | 400.4 | 0.1432 |
| Black | 113 | 31.14 | 215.1 |
| Mixed | 204 | 111.2 | 77.37 |
| Other | 272 | 66.74 | 631.3 |
The \(\chi^2\) values for each group are added together to give the overall \(\chi^2\)-test statistic. \[\chi_{stat}^2 = 6.939 + 0.1432 + 215.14 + 77.37 + 631.3 = 930.9\]
As with other hypothesis tests, the larger the test statistic, the stronger the evidence against \(H_0\). Therefore, we wish to know if this test statistic (i.e. \(\chi_{stat}^2 = 930.9\)) is considered large, if the null hypothesis is true. To determine this, we compare it to a reference distribution; not surprisingly, for a \(\chi^2\) test, the reference distribution is a \(\chi^2\) distribution. The \(\chi^2\) distribution is indexed by one parameter, the degrees of freedom, found from (for a one-way table):
\[\textrm{df} = \textrm{number of categories} - 1 \]
The \(\chi^2\) distribution takes different shapes according to the degrees of freedom. You can explore these in Figure 12.1. There is also a live version here
Figure 12.1: Exploring the \(\chi^2\) distribution. You can see a live version by clicking here
We have 5 ethnic groups and so
\[\textrm{df} = 5 - 1 = 4\] The reference distribution (\(\chi^2_{df=4}\)) is shown in Figure 12.2.
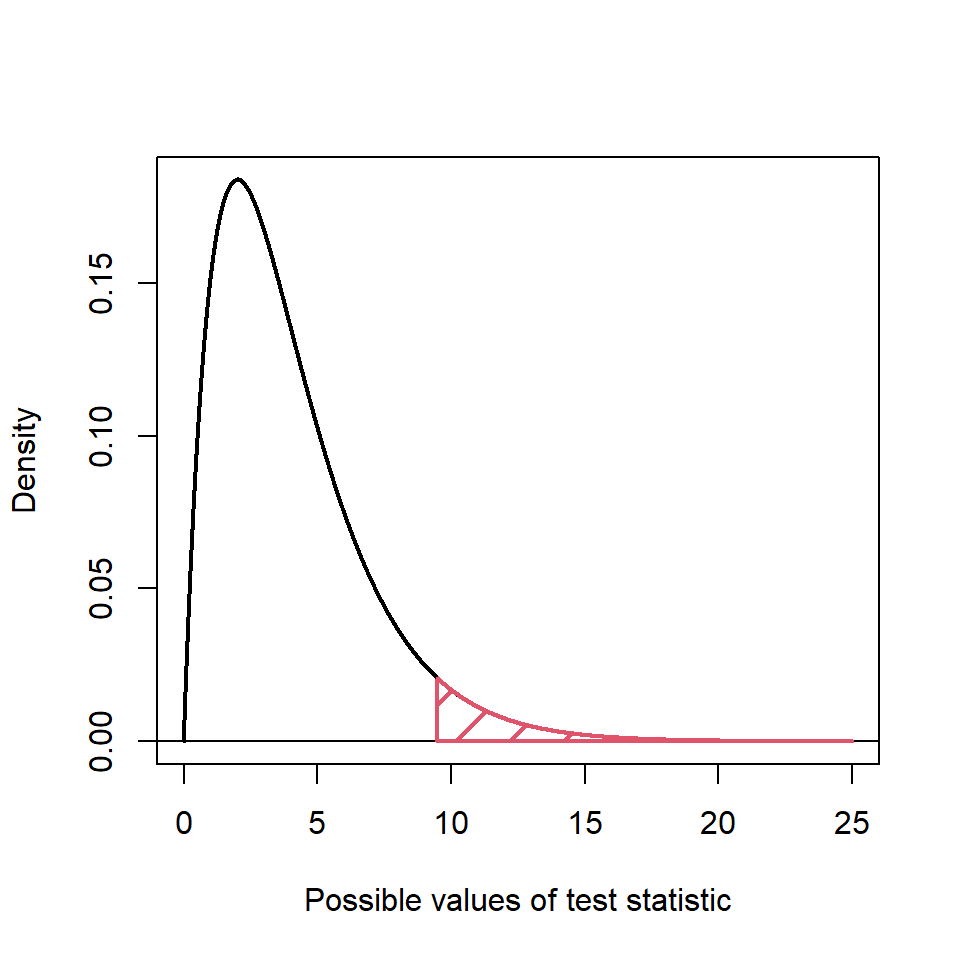
Figure 12.2: Reference distribution, \(\chi^2_{df=4}\). The red shaded area shows the critical region, testing at a 5% significance level. Note that only one tail is used.
We can see that values most likely to occur are around 2 to 6 and testing at a significance level of 5%, the critical value is 9.49. Hence, a value of 930.9 is very untypical and, indeed the exact probability associated with this test statistic is pretty much zero. Hence, we have strong evidence against \(H_0\); the observed numbers in the ethnic groups from the sample do not represent what we would expect according to the census.
We can go further and investigate what gave rise to such a large test statistic; \(\chi^2\) components for the Black and Other groups were particularly large. The observed number in the Other group was 272 pupils, but according to the census, we expected 67 pupils in this group, hence this large discrepancy led to the large \(\chi^2\) component. Thus, pupils identified as Other and Black were over-represented in the sample compared to the population. This may be due to biased sampling or changing demographics in the population.
12.2.1 Doing this in R
To perform a \(\chi^2\) test in R, we need to provide the observed values and the proportions under the null hypothesis (note, the proportions need to sum to 1).
# Groups
Group <- c("White","Asian","Black","Mixed","Other")
# Observed frequencies from SALSUS
Frequency <- c(21249, 408, 113, 204, 272)
# Proportions in each group from census
CensusProp <- c(0.9726, 0.018, 0.0014, 0.005, 0.003)
# Chi-square test - save to new object
salsusTest <- chisq.test(x=Frequency, p=CensusProp)
salsusTest
Chi-squared test for given probabilities
data: Frequency
X-squared = 930.91, df = 4, p-value < 2.2e-16The new ‘test statistic’ object contains some useful information, such as the expected values:
# Expected values
salsusTest$expected[1] 21636.4596 400.4280 31.1444 111.2300 66.7380Unfortunately, the test statistic object does not contain the \(\chi^2\) components but these can easily be calculated:
# Save expected values
Expected <- salsusTest$expected
# Chi-square values for each group
(Frequency - Expected)^2/Expected[1] 6.9385169 0.1431848 215.1378499 77.3736663 631.3118260The critical value associated with testing at a fixed significance level can be found using the following command. Note that the distribution is not symmetric and so we want the area in the right hand tail.
# Critical value, testing at a 5% significance level
qchisq(p=0.05, df=4, lower.tail=FALSE)[1] 9.487729The exact \(p\)-value can be found using:
# Exact p-value for test statistic
pchisq(q=930.9, df=4, lower.tail=FALSE)[1] 3.360768e-200Q12.1 A curious child was interested in determining whether a six-sided die was fair and threw the die 60 times and recorded the result each time. The observed frequency distribution is given below.
| Number | Frequency |
|---|---|
| 1 | 8 |
| 2 | 7 |
| 3 | 9 |
| 4 | 19 |
| 5 | 7 |
| 6 | 10 |
a. State the null and alternative hypotheses for a chi-square goodness-of-fit test.
b. For the null hypothesis is part a, what are the expected values?
c. Calculate a suitable test statistic.
d. Using the following information, what do you conclude?
qchisq(p=0.05, df=5, lower.tail=FALSE)[1] 11.0705e. The child is not convinced by these results of the statistical test. What might they do to convince themselves?
12.3 \(\chi^2\) test of independence
Previously we described a test for a one-way table. Sometimes we have a cross-tabulation, or two-way table. Consider the following data (Table 12.5) tabulating support for Democratic, Republican or Independent candidates by gender (taken from (Agresti 2007)).
| Gender | Democrat | Independent | Republican |
|---|---|---|---|
| Female | 762 | 327 | 468 |
| Male | 484 | 239 | 477 |
In total there are 2,757 individuals in the sample. A question that might arise is whether there is more female support for Democrats than Republicans, for example. Indeed there are more female supporters for Democrats than Republicans in our sample, but there were also more Democrats in the sample. Even adjusting for this, another sample would give different frequencies and so is the difference explicable by sampling variability or is there a relationship between political support and gender? We wish to determine whether there is a relationship, or association, between political support and gender or whether gender and political support are independent of one another.
The null hypothesis we test assumes that the two variables are independent (hence a test of independence). In this example, the null hypothesis is:
\[H_0: \textrm{gender and voting intention are independent}\]
The alternative hypothesis states the opposite view.
\[H_1: \textrm{gender and voting intention are not independent, i.e. there is an association}\]
As before, we calculate expected counts assuming that \(H_0\) is true. In this case, the probability of being in a particular cell, is the probability of being in the particular row, multiplied by the probability of being in the particular column (remember \(P(A \cap B) = P(A) \times P(B)\) for independent events). Thus, the expected count for each cell in the table is given by
\[\textrm{Expected value} = \frac{\textrm{row total}}{\textrm{grand total}} \times \frac{\textrm{column total}}{\textrm{grand total}} \times \textrm{grand total}\] where the grand total is the overall total (or sample size). Some values can be cancelled out and so the formula is abbreviated to:
\[\textrm{Expected value} = \frac{\textrm{row total} \times \textrm{column total}}{\textrm{grand total}} \] To use this formula in our example, we need the necessary totals (Table 12.6).
| Gender | Democrat | Independent | Republican | Total |
|---|---|---|---|---|
| Female | 762 | 327 | 468 | 1557 |
| Male | 484 | 239 | 477 | 1200 |
| Total | 1246 | 566 | 945 | 2757 |
Thus, the expected number of female Democrat supporters is:
\[\textrm{Expected value} = \frac{1557 \times 1246}{2757} = 703.67\]
The expected number of male Democrat supporters is:
\[\textrm{Expected value} = \frac{1200 \times 1246}{2757} = 542.33\]
We do this for all cells in the table (Table 12.7):
| Gender | Democrat | Independent | Republican |
|---|---|---|---|
| Female | 703.7 | 319.6 | 533.7 |
| Male | 542.3 | 246.3 | 411.3 |
As before, the test statistic (\(\chi_{stat}^2\)) is given by
\[\chi_{stat}^2 = \sum_{\textrm{all cells}} \frac{(\textrm{O} - \textrm{E})^2}{\textrm{E}}\]
The chi-square component for the female Democrat supporters is thus:
\[\frac{(762 - 703.67)^2}{703.67} = 4.84\]
The chi-square values for all cells are shown in Table 12.8.
| Gender | Democrat | Independent | Republican |
|---|---|---|---|
| Female | 4.835 | 0.169 | 8.084 |
| Male | 6.273 | 0.22 | 10.49 |
Thus, the test statistic is:
\[\chi^2_{stat} = 4.835 + 0.169 + 8.084 + 6.273 + 0.220 + 10.489 = 30.07\]
We need to compare this to a \(\chi^2\) reference distribution; the degrees of freedom are found from:
\[ \textrm{df} = (\textrm{number of rows}-1) \times (\textrm{number of columns}-1) \]
The data in this example is a \(2 \times 3\) table, thus the degrees of freedom are: \[ df = (2-1) \times (3-1) = 2\]
The reference distribution, \(\chi^2_{df=2}\), is shown in Figure 12.3.
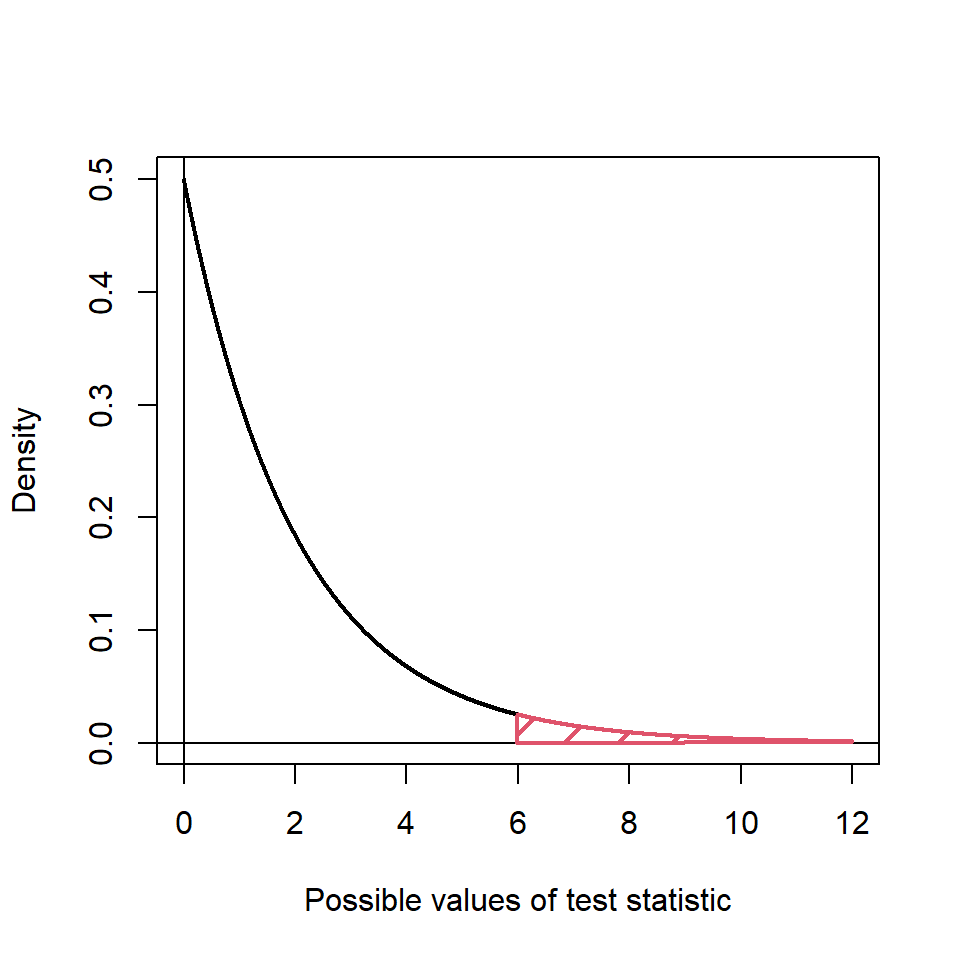
Figure 12.3: Reference distribution, \(\chi^2_{df=2}\). The red shaded area shows the critical region, testing at a 5% significance level.
The red shaded area in Figure 12.3 indicates that the critical value is 5.99 and so since the test statistic is greater than this, we reject the null hypothesis. There is evidence to suggest that gender is not independent of political support.
If we examine the \(\chi^2\) components (Table 12.8), we see that the largest components were for Republicans and then Democrats. There were less female Republicans and more male Republicans than expected given the null hypothesis; the converse was true for Democrats.
12.3.1 Doing this in R
The key to performing a \(\chi^2\) test of independence is getting the data into the correct matrix form and so it is useful to print it out before going ahead with the test.
# Create data
voters <- c(762,327,468,484,239,477)
# Convert to a matrix
voters.mat <- matrix(voters, nrow=2, ncol=3, byrow=TRUE)
voters.mat [,1] [,2] [,3]
[1,] 762 327 468
[2,] 484 239 477# Chi-square test of independence
chisq.test(x=voters.mat)
Pearson's Chi-squared test
data: voters.mat
X-squared = 30.07, df = 2, p-value = 2.954e-07Note that for 2 \(\times\) 2 tables, a correction is applied by default in the chisq.test function. The reason for this is that we assume a discrete distribution can be approximated by continuous distribution (i.e. the \(\chi^2\) distribution). To account for this approximation, an adjustment is made to the formula to calculate \(\chi_{stat}^2\) which makes the test statistic smaller, and thus the corresponding \(p\)-value will be larger.
Q12.2 A student newspaper (The Saint, 02/02/2019) conducted a survey using social media platforms to determine whether students were in favour of the UK holding a second referendum on Brexit. A statistics student wanted to determine whether voting preference was different on the two social media platforms. The numbers of students who voted are given in the following table.
| Platfom | Yes | No |
|---|---|---|
| 158 | 61 | |
| 19 | 11 |
a. State a suitable null and alternative hypothesis of a statistical test to determine whether voting preference was different between the social media platforms.
b. Calculate the expected counts, assuming that voting preference was not related to social media platform.
c. Calculate an appropriate test statistic for the test described in part (a).
d. If the exact \(p\)-value associated with the test statistic calculated in part (c) was 0.32, what do you conclude?
12.4 Test assumptions
As with other hypothesis tests, \(\chi^2\) tests require that some assumptions are fulfilled in order that the results are reliable.\(\chi^2\) tests are only valid when the data are collected as a random sample or as a number of random samples. They are ‘large’ sample tests that require the total count for the table to be sufficiently large. The following rules of thumb help ensure we don’t use \(\chi^2\) tests for samples which are too small:
- each expected cell count should be greater than 1
- 80% (at least) of the expected counts should be at least 5.
If these rules do not hold, then the categories may be combined in some sensible way to achieve acceptable cell counts.
12.5 Summary
Although discrete data are summarised and treated differently to continuous data, the approach to hypothesis testing is the same; the null and alternative hypotheses are stated, a test statistic is calculated and then compared to a reference distribution. \(\chi^2\) tests are used for discrete data in the form of contingency tables.
12.5.1 Learning outcomes
In this chapter you have seen how to undertake a:
test for goodness of fit to some distribution, and
test for independence/association.
12.6 Answers
Q12.1 In this example, we conduct a goodness-of-fit test to check whether the die is fair.
Q12.1 a. The hypotheses could be specified in a variety of ways, for example
\[H_0: \textrm{all numbers are equally likely} \] \[H_1: \textrm{the numbers are not equally likely to occur}\]
Q12.1 b. The total number of throws was 60. Thus, if each number is equally likely (i.e. with probability \(\frac{1}{6}\)) we would expect each number to be thrown 10 times (for a sample of size 60).
Q12.1 c. The \(\chi^2\) test statistic is given by:
\[\chi_{stat}^2 = \sum_{\textrm{all cells}} \frac{(\textrm{O} - \textrm{E})^2}{\textrm{E}}\] The \(\chi^2\) values are:
| Number | Frequency | Expected | Chi |
|---|---|---|---|
| 1 | 8 | 10 | 0.4 |
| 2 | 7 | 10 | 0.9 |
| 3 | 9 | 10 | 0.1 |
| 4 | 19 | 10 | 8.1 |
| 5 | 7 | 10 | 0.9 |
| 6 | 10 | 10 | 0 |
The \(\chi^2\) test statistic is
\[\chi_{stat}^2 = 0.4 + 0.9 + 0.1 + 8.1 + 0.9 + 0 = 10.4\]
Q12.1 d. The test statistic is compared to a reference distribution; with six categories, df \(= 6 - 1 = 5\). The information provided in the R output was a critical value, testing at a significance level of 5% (i.e. \(\chi^2_{crit}=11.07\)). The test statistic is smaller (but not by much) than the critical value, thus these data do not provide evidence to reject the null hypothesis. We conclude that the die is fair.
dieFreq <- c(8, 7, 9, 19, 7, 10)
# Note, no need to specify proportions if expected cell proportions are equal
chisq.test(x=dieFreq)
Chi-squared test for given probabilities
data: dieFreq
X-squared = 10.4, df = 5, p-value = 0.06466Q12.1 e. The child could increase the sample size with more throws of the die.
Q12.2 This question calls for a \(\chi^2\) test of independence.
Q12.2 a. The hypotheses are:
\(H_0\): Voting preference is independent of social media platform (i.e. no difference in voting preference between platforms)
\(H_1\): Voting preference is not independent of the social media platform (i.e. voting preference is different between platforms).
Q12.2 b. The expected counts in each cell in the table are given by
\[\textrm{Expected value} = \frac{\textrm{row total} - \textrm{column total}}{\textrm{grand total}}\] The totals are
| Platfom | Yes | No | Total |
|---|---|---|---|
| 158 | 61 | 219 | |
| 19 | 11 | 30 | |
| Total | 177 | 72 | 249 |
The expected values are
| Platfom | Yes | No |
|---|---|---|
| 155.7 | 63.33 | |
| 21.33 | 8.675 |
Q12.2 c. The chi-square test statistic is given by
\[\chi_{stat}^2 = \sum_{\textrm{all cells}} \frac{(\textrm{O} - \textrm{E})^2}{\textrm{E}}\]
| Platfom | Yes | No |
|---|---|---|
| 0.0347 | 0.0854 | |
| 0.2535 | 0.6233 |
Summing the \(\chi^2\) values gives the test statistic:
\[ x_{stat}^2 = 0.0347 + 0.0854 + 0.2535 + 0.6233 = 0.9969\]
Q12.2 d. Given that the \(p\)-value is 0.32 (much greater than a 5% significance level), there is no evidence to reject the null hypothesis and conclude that the two factors are independent, i.e. that voting preference is independent of choice of social media platform.
voteFreq <- c(158, 61, 19, 11)
voteFreq.mat <- matrix(voteFreq, nrow=2, byrow=TRUE)
# Without correction
chisq.test(x=voteFreq.mat, correct=FALSE)
Pearson's Chi-squared test
data: voteFreq.mat
X-squared = 0.99698, df = 1, p-value = 0.318# With correction
chisq.test(x=voteFreq.mat)
Pearson's Chi-squared test with Yates' continuity correction
data: voteFreq.mat
X-squared = 0.61432, df = 1, p-value = 0.4332