Chapter 11 Proportions
There is no excellent beauty that hath not some strangeness in the proportion. Sir Francis Bacon (1696)
11.1 Introduction
Data often come as counts or frequencies which can be transformed to proportions. For example, imagine a survey where at each of several locations, the presence or absence of one or more birds is noted. The proportion of locations where a bird was located can be obtained from
\[\textrm{proportion of bird locations} = \frac{\textrm{number of locations where one or more birds are seen}}{\textrm{total number of locations}}\]
We can use the observed proportion to estimate the probability of seeing one or more birds at a particular locality, \(x\), out of the number of trials, \(n\), to estimate the probability of success, \(p\):
\[\hat p = \frac{x}{n}\]
Hence, we estimate the true underlying probability \(p\) with the sample proportion \(\hat p\). If different locations had been sampled, then the observed proportion of locations where a bird was detected would likely change. There is some uncertainty associated with the sample proportions. Therefore in this chapter we consider:
- confidence intervals for proportions
- confidence intervals for a difference in proportions and
- a hypothesis test for a proportion.
Proportions and probabilities are similar in that they are both bounded by 0 and 1 and the terms are often used interchangeably, not least because the sample proportion is frequently used to estimate the underlying (but unknown) population probability of success.
In some cases, looking at the difference between proportions is not possible or relevant and so a ratio is obtained - this is called an odds ratio and discussed at the end of this chapter.
11.2 Confidence intervals
To illustrate the formulation of CI for a proportion, we can consider the bird survey mentioned above. Imagine the birds were surveyed at three different time periods (perhaps before (which we will call phase A), during (phase B) and after (phase C) the building of a windfarm. There are two obvious questions of interest: in what proportion of localities will a bird be seen and what is the difference in the proportion of birds seen between the phases?
To estimate the proportion of localities with birds in this region assume that the number of locations where a bird was detected \(x\) is a random variable from a binomial distribution with known \(n\) (fixed number of trials, i.e. all sampling locations) and unknown \(p\) (probability of success).
We will estimate the proportion of ‘successful’ observations, \(p\), from the number of observations with sightings (‘successes’) and the total number of observations (`trials’).
Recall, there are 4 conditions of the binomial distribution:
- two outcomes for each trial,
- the same probability of success for each trial,
- a fixed number of trials,
- independence of trials.
Q11.1 How realistic are these conditions for the wind farm data?
11.2.1 Motivating example
Trained observers recorded the presence or absence of birds at each spatial location:
- when birds were seen in some defined location a presence (success) was recorded
- and when birds were not seen it was recorded as an absence (failure).
We estimate the probability of sighting an animal using:
\[\hat{p}=\frac{\text{number of successes}}{\text{number of trials}} \]
which in the wind farm data, as mentioned in the introduction, translates to:
\[\hat p = \frac{\textrm{number of observations where one or more birds were seen}}{\textrm{total number of observations}}\] For each phase we have the number of successful observations and the number of observations in total (Table 11.1).
| A | B | C | |
|---|---|---|---|
| 0 | 10335 | 12495 | 5436 |
| 1 | 1143 | 1633 | 460 |
| Total | 11478 | 14128 | 5896 |
\[\hat p_{A} = \frac{1143}{11478} = 0.0996 \quad; \quad \hat p_{B} = \frac{1633}{14128} = 0.1156 \quad ; \quad \hat p_{C} = \frac{460}{5896} = 0.0780\] We can estimate similar probabilities for each year and month (Figure 11.1) of the survey. The before period was from 2000 to 2002 inclusive, the during period was 2003 and 2007 and the after period was 2011.
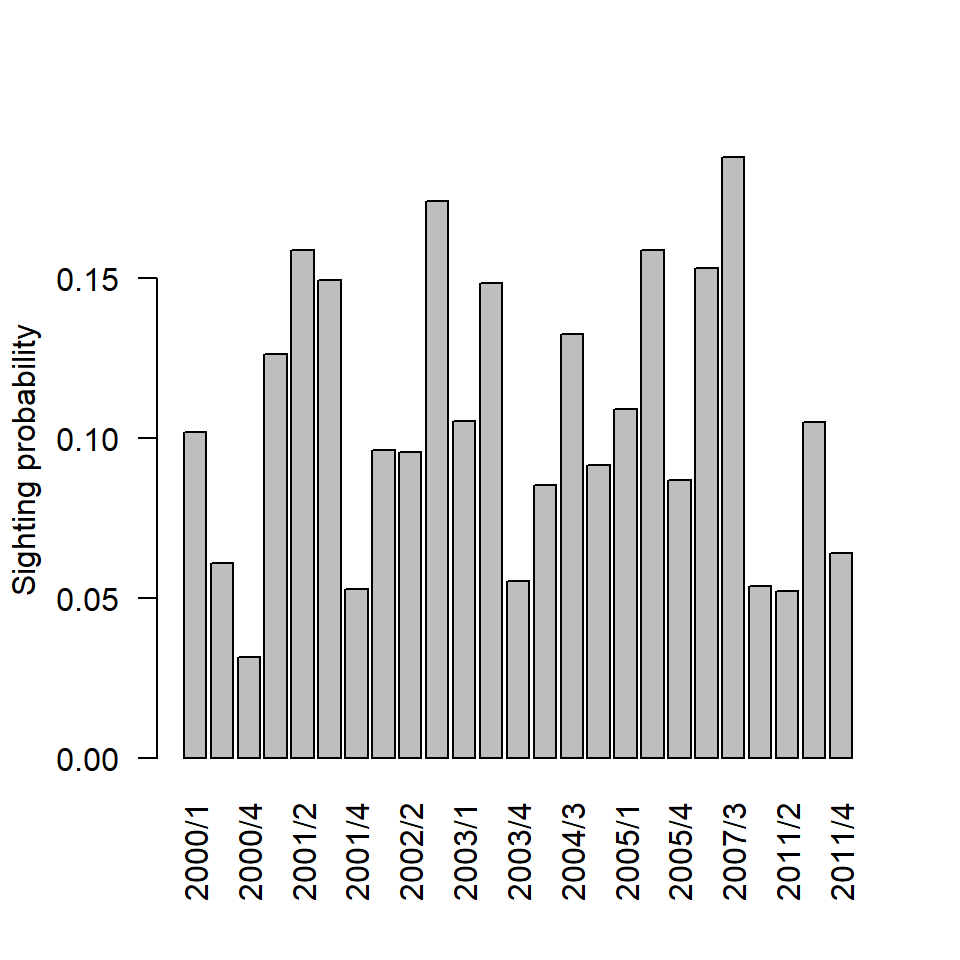
Figure 11.1: Barplot showing the mean sightings probability for every year/month combination. N.B.Not all months are labelled
From this information (Figure 11.1) we see that:
- the proportion of sighting a bird appears to be higher in phase B compared with the phases A and C,
- and the proportion of sighting a bird tends to be highest in January-March of each year.
While some patterns are apparent, it is difficult to tell if the observed differences are genuine differences across phases and/or year-month combinations or if these differences are due to sampling error; would these differences have been seen even if the true underlying (but unknown) probability of sighting for all phases (and/or year-month combinations) was the same? To assess the uncertainty associated with a sample proportion, we build a confidence interval and the formulation of the interval depends on the number of trials, \(n\), and on the value of \(p\).
11.2.2 Confidence intervals: large sample sizes
While the number of successes from the number of trials is assumed to be a binomial random variable, the sample proportions (estimates for \(p\); \(\hat{p}\)) are normally distributed about the true (underlying) population proportion if the number of trials is large. Therefore, confidence intervals (CIs) for proportions are constructed in a similar way to CIs for large samples of normal data. For large samples, the sample proportion is approximately normally distributed:
\[\hat{p} \sim normal \left(p, se({p})\right)\] However, since we never know \(p\), we use the sample proportion \(\hat p\), thus, the standard deviation of the sample proportion (the standard error) can be found using:
\[se(\hat{p})=\sqrt{\frac{\hat p (1-\hat p)}{n}}\] Just as with means we can create 95% confidence interval on the proportions.
To find a 95% confidence interval for \(p\) we use a familiar structure: \[\begin{align*} \textrm{estimate}~~ &\pm z_{1-\frac{\alpha}{2}} \times~~ \textrm{standard error}\\ \hat{p} & \pm 1.96 \times \sqrt{\frac{\hat{p} (1-\hat{p})}{n}} \end{align*}\]
where \(\alpha=0.05\) for a 95% CI, hence \(z_{0.025}\).
11.2.2.1 How large is large enough?
To assume these estimates are approximately normally distributed about \(p\) we require large samples. As the number of trials increases, the distribution becomes more and more like the normal distribution until the sample size is so large that the distribution is exactly normally distributed - it has reached a limit, or asymptote, hence, these CI are sometimes called ‘asymptotic’ confidence intervals. However, the required sample size changes with \(\hat{p}\).
The minimum sample sizes for different values of \(\hat p\) are given in Table 11.2. Thus if p is very small 0.05 or large 0.95, a sample size of at least 960 would be required in order to assume that the proportion is normally distributed.:
| Value for \(\hat{p}\) | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 |
|---|---|---|---|---|---|---|---|---|---|---|
| Minimum \(n\) | 960 | 400 | 220 | 125 | 76 | 47 | 23 | 13 | 11 | 10 |
| Value for \(\hat{p}\) | 0.95 | 0.9 | 0.85 | 0.8 | 0.75 | 0.7 | 0.65 | 0.6 | 0.55 | 0.5 |
Example We are going to build 95% CIs for the proportion of sighting birds in phases A, B and C. The total number of sampled locations (\(n\)) for each phase is greater than 1000 and so results based on these large-sample properties should be valid.
The CI for Phase A is constructed as follows: we estimated \(p_A\) previously, \(\hat p_A = 0.0996\) and the standard error is given by:
\[se(\hat{p_A})=\sqrt{\frac{\hat{p_A}(1-\hat{p_A})}{n}}= \sqrt{\frac{0.0996(1-0.0996)}{11478}}= 0.0028\]
\[\begin{align*} 95\%~ \textrm{CI}=&\hat{p} \pm z_{0.025} \times se(\hat{p})\\ =&0.0996 \pm 1.96 \times 0.0028\\ =& (0.0941,0.1051) \end{align*}\]
Based on these results we can be 95% confident that the proportion of locations with a bird in Phase A is somewhere between 0.094 (9.4%) and 0.105 (10.5%).
We find 95% CI for the proportions in phases B and C and thus can say,
with 95% confidence we estimate the proportion of a location with a bird in this region in Phase B to be somewhere between 0.11, 0.121
with 95% confidence we estimate the proportion of a location with a bird in this region in Phase C to be somewhere between 0.071, 0.085.
11.2.2.2 Doing this in R
To calculate these confidence intervals in R, an additional package is required Hmisc (Harrell 2021):
# Load package
library(Hmisc)
# 95% CI using asymptotic normal approximation; x=number of successes;
# n=number of trials
binconf(x=1143, n=11478, alpha=0.05, method="asymptotic") PointEst Lower Upper
0.09958181 0.09410374 0.105059911.2.3 Confidence intervals: small sample sizes
For ‘small’ samples (less than those in the table above) when \(p\) is close to zero or one, assuming the proportions are normally distributed is not valid.
To illustrate this we calculate the 95% CI for \(\hat p=0.1\) and \(n=10\).
\[se(\hat p) = \sqrt{\frac{0.1 (1-0.1)}{10}} = 0.0949\]
Hence, the CI is given by
\[0.1 \pm 1.96*0.0949\] \[0.1 \pm 0.1859 \] \[-0.086 \quad ; \quad 0.286 \]
The lower limit is less than 0 and a proportion cannot be negative. Therefore, a different formulation is required for small sample sizes.
The literature suggests that Wilson intervals are preferred in these cases (Agresti and Coull 1998). This has a rather more complicated formula:
\[\frac{1}{1+{\frac{1}{n}}z^{2}}\left[{\hat {p}}+{\frac{1}{2n}}z^{2}\pm z{\sqrt{{\frac {1}{n}}{\hat{p}}\left(1-{\hat{p}}\right)+{\frac {1}{4n^{2}}}z^{2}}}\right]\]
(and so we will be using R to calculate these values.)
This approach ensures that the confidence interval limits never extend below zero or above one.
For example, Table 11.3 the asymptotic (i.e. using the normal distribution) and Wilson confidence intervals are calculated when we have one success and 10 trials (i.e. \(p=0.1\)):
| PointEst | Lower | Upper | |
|---|---|---|---|
| Wilson | 0.1 | 0.005129 | 0.4042 |
| Asymptotic | 0.1 | -0.08594 | 0.2859 |
The lower limit for the confidence interval based on the normal distribution is negative - an implausible value for a proportion.
According to our table of ‘what is large,’ when \(\hat{p} = 0.1\), we should have a sample size of more than 400 to use the method based on the normal distribution.
If we increase the number of trials to 1000, (and the number of success to 100 so that \(\hat{p}=0.1\)), then the asymptotic normal distribution-based interval no longer gives impossible values (Table 11.4).
| PointEst | Lower | Upper | |
|---|---|---|---|
| Wilson | 0.1 | 0.08291 | 0.1202 |
| Asymptotic | 0.1 | 0.08141 | 0.1186 |
However, note that for very small estimates of \(p\), Wilson intervals are still preferred even if the number of trials is large.
For our wind farm data, the Wilson intervals for the proportions of locations are given in in Table 11.5:
| Phase | PointEst | Lower | Upper |
|---|---|---|---|
| A | 0.09958 | 0.09424 | 0.1052 |
| B | 0.1156 | 0.1104 | 0.121 |
| C | 0.07802 | 0.07144 | 0.08514 |
These are very similar to the CI we calculated earlier; this is not surprising since the numbers of trials are so large.
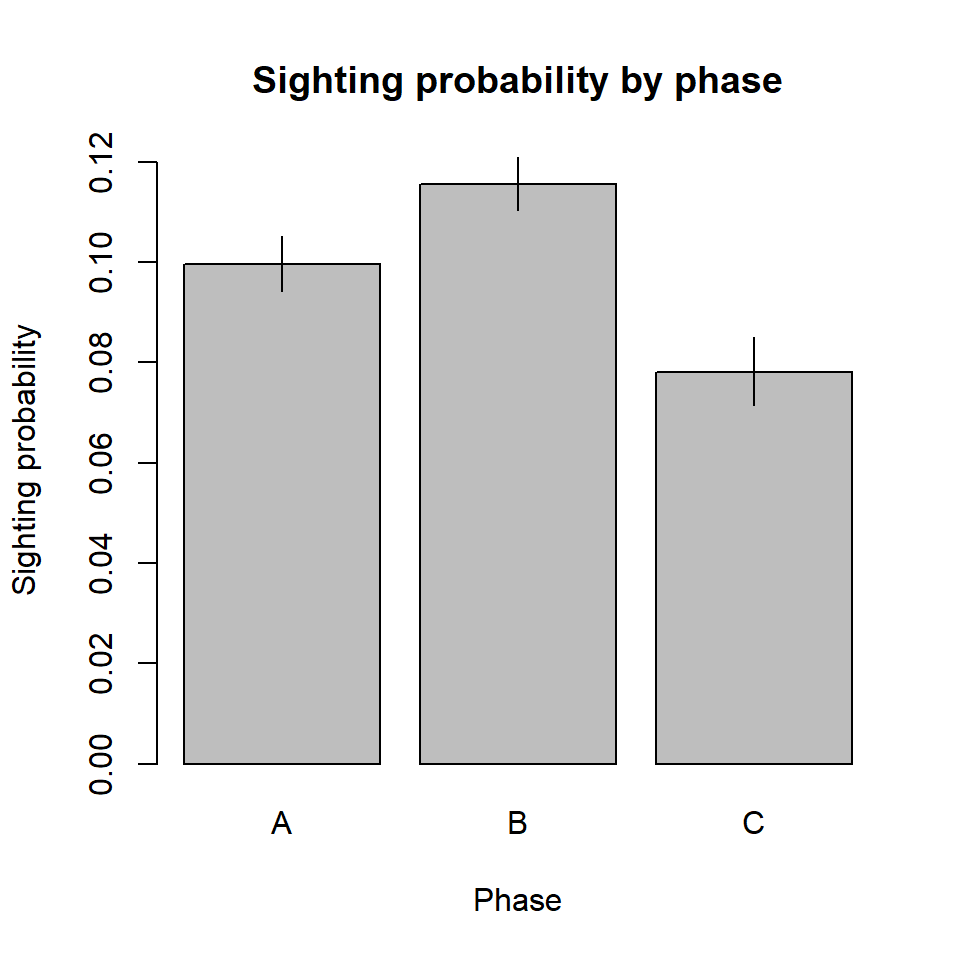
Figure 11.2: Barplot showing the mean sightings probability for each of the three phases. The black lines are 95% Wilsons confidence intervals.
11.2.3.1 Doing this in R
Wilson confidence intervals are obtained by specifying method="wilson.
# Wilson's CI for p=0.1 and number of trials is 10
binconf(x=1, n=10, alpha=0.05, method="wilson") PointEst Lower Upper
0.1 0.005129329 0.4041511.3 Comparing two proportions: the \(z\) test
In this section we compare two proportions and again use the wind farm data as a motivating example.
While there appears to be some differences across phases based on the results obtained so far, in order to statistically answer questions about changes in proportions over time, we need to formally test for differences between the groups (e.g. between phases or between different years or months).
Rather than use confidence intervals, which give a range of likely values for each parameter, we test for no difference between the two parameter values and evaluate the strength of evidence against this null hypothesis. We formally compare two proportions with a hypothesis test, which uses the normal distribution as the reference distribution (known as a \(z\) test).
So for example, we examine if there have been changes between phases in the windfarm data by comparing the differences we have observed between phases with the sorts of differences we would expect to see even if no genuine changes have occurred.
11.3.1 Testing for ‘no difference’ between groups
In order to test the research hypothesis that sighting proportions were different in phase A (\(p_{A}\)) and phase C (\(p_{C}\)) we take the following steps:
- We test this research hypothesis using the (skeptical) null hypothesis of no difference (\(H_0\)) and a `two-sided’ alternative hypothesis (\(H_1\)) of either a positive or negative difference:
\[H_0: p_{A}-p_{C}=0\]
\[H_1: p_{A}-p_{C} \neq 0\]
We evaluate the null hypothesis by considering what we would expect to see if the null hypothesis is true. For example,
- if there has been no difference in sighting probabilities between phases then we would expect to see small differences in the sighting rates across phases.
- small differences like these (based on sampling variability alone) provide us with the background for comparison with the differences we did observe across phases.
We compare our data-estimate (i.e. the difference between \(p_{A}\) and \(p_{C}\)) with the hypothesised value (for no difference, or zero, in this case):
\[\textrm{data-estimate} - \textrm{hypothesised value}\]
- Our data-estimate for the difference between the proportions is:
the hypothesised value is 0, therefore our estimate is 0.0216 units.
While the point estimate (of 0.0216) is useful, we know that if we had taken data from slightly different locations or at slightly different times we would have obtained a different set of data and so we need to consider the uncertainty in our estimate.
The uncertainty in the estimate of the difference between the proportions can be quantified by the standard error of the difference:
\[\begin{align*} se(\hat{p}_A-\hat{p}_C)=&\sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_C(1-\hat{p}_C)}{n_C}}\\ \end{align*}\]
\[\begin{align*} =& \sqrt{\frac{0.0996(1-0.0996)}{11478}+\frac{0.078(1-0.078)}{5896}}\\ = & 0.004\\ \end{align*}\]
This method of calculating the uncertainty in our estimate (the standard error formula) requires these sample proportions are independent.
Do you think this is realistic in this case?
11.3.1.1 How does our estimate compare with the differences we might expect?
Once we have quantified the uncertainty about our estimate we can represent the difference seen between sample proportions as a ratio of the standard error.
\[\text{test statistic} = \frac{\text{difference - hypothesised value}}{\text{standard error}}\]
This puts our estimate for the difference into perspective:
small differences can look large if the standard error is small (and our estimate has high precision/low uncertainty) and
large differences can look small (if our estimate has low precision/high uncertainty).
In our example, even an apparently small difference is actually large when we consider the high precision/low uncertainty about the estimate:
\[\begin{align*} \textrm{test statistic} =&\frac{\textrm{difference-hypothesised value}}{\textrm{standard error}}\\ =& \frac{0.022}{0.004} = 4.82\\ \end{align*}\]
This estimate is in excess of 4 standard errors above zero. This can be seen in Figure 11.3; where the test statistic is compared to the reference distribution i.e. a distribution that we might expect to see (because of sampling variability) even if there is no underlying difference in the values of the true proportions.
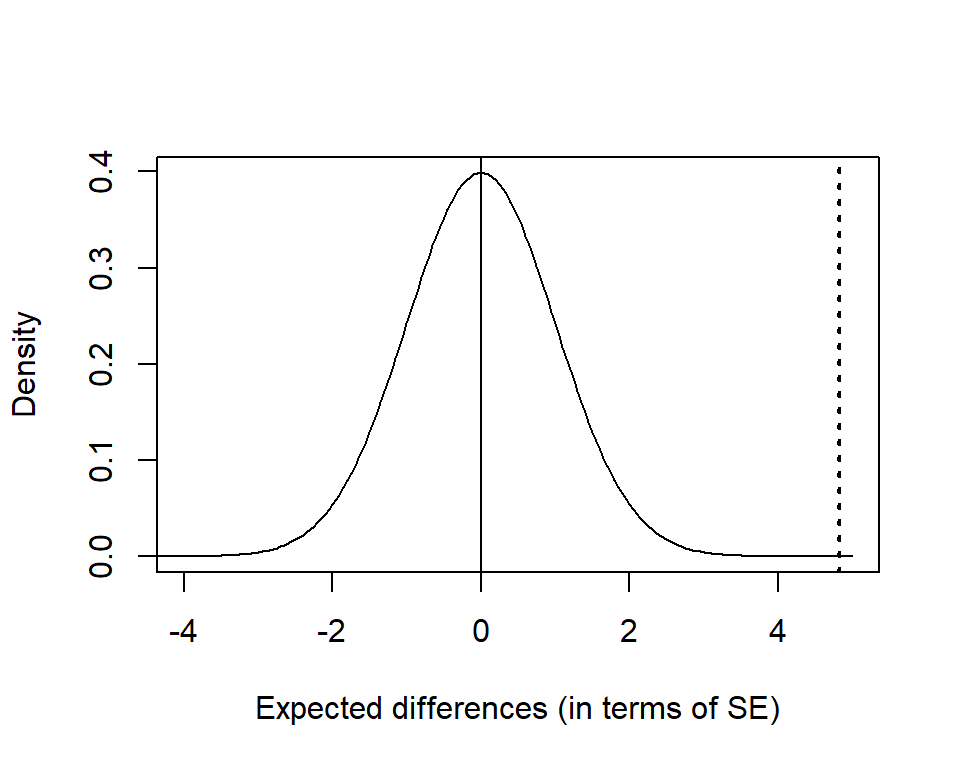
Figure 11.3: Reference distribution for the \(z\) test: the differences between proportions that would be expected if \(p_1=p_2\). The dotted line indicates the test statistic.
From here we can evaluate the chance of getting a value at least as extreme as 4.82 when \(H_0\) is true and there was no difference in proportions across phases.
We do this using the normal distribution as a reference distribution because it turns out that when there are no differences across phases, the test statistic has a normal distribution with \(\mu=0\) and \(\sigma=1\). This distribution is known as the standard normal distribution or \(z\) distribution (Chapter 8).
We use this reference distribution as a comparison with our observed test statistic.
In this case, we find the chance of seeing a difference like this (or one more extreme) is very small: the probability is \(10^{-6}\).
What can we conclude?
We have strong evidence for a difference between the proportions of locations where birds were detected in phase A and phase C.
We can reject the null hypothesis of no difference between proportions in phase A and phase C at the 1% level.
- Specifically, the probability of sighting a bird in Phase C appears to be significantly lower than in Phase A.
11.4 CI for the difference between population proportions, (\(p_1-p_2\))
In the wind farm example we are interested in asking if there are differences across phases.
We can calculate the confidence interval for the difference in two proportions in the standard way:
\[\textrm{difference between sample proportions} \pm z\textrm{-multiplier} \times \textrm{standard error of the difference}\]
\[(\hat p_1-\hat p_2) \pm z_{1-\frac{\alpha}{2}} \times se(\hat p_1-\hat p_2)\]
However, the choice of formula for the standard error of the difference between two proportions can be important.
For instance, it might be unrealistic to assume independence between samples and so the standard error formula used previously (situation A - see later) might be inappropriate.
For this reason (and in lots of other situations) we may need to use a different formula to calculate the standard error, which acknowledges that both sample proportions are estimated from a common sample.
In our example, it is possible that the proportions of locations where birds were detected in each phase are not independent because the two phases are likely to ‘share’ animals. Similarly, the locations within each phase may not be independent, in that if there are birds in one location, birds may be more likely to be in nearby locations.
11.4.1 Choosing the appropriate standard error when comparing proportions
When comparing proportions difference sorts of sampling situations can arise. This means that different standard errors should be used. The sampling situations we consider here are:
Situation A - the proportions originate from independent samples.
Situation B - the same sample gives rise to two (or more) proportions where the same individual can only choose one of the options (or can only contribute to ONE of the proportions being considered).
Situation C - the same sample but an individual can choose more than one category (or can contribute to BOTH of the proportions being considered).
11.4.1.1 Situation A: Proportions from independent samples
Example A random sample of 1000 people born in New Zealand is compared to a random sample of 1000 people born in Scotland, e.g. a respondent can’t belong to both populations.
\[se(p_1-p_2) = \sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\]
11.4.1.2 Situation B: One sample of size \(n\), several response categories
Example A random sample of Scots are asked who they are going to vote for in the next election, e.g. one group of respondents slot into only ONE category and the proportions add to 1.
\[se(p_1-p_2) =\sqrt{\frac{p_1+ p_2-(p_1-p_2)^2}{n}}\]
11.4.1.3 Situation C: One sample of size \(n\), many “Yes/No” items
Example A random sample of Scots are asked: 1. Do you watch rugby? 2. Do you like beer? 3. Do you like licorice? e.g. one group of respondents can slot into MORE THAN ONE category.
\[se(p_1-p_2) = \sqrt{\frac{Min(p_1 + p_2, q_1 + q_2)-(p_1-p_2)^2}{n}}\]
where \(q_1 = 1-p_1\) and \(q_2 = 1-p_2\) and \(Min(a, b)\) denotes selecting the minimum from \(a\) or \(b\).
The following graphics from Wild & Seber(1999) may help visualise these situations.
11.4.1.4 Choosing different standard errors
As an illustration of which standard error to choose, we consider the data from an international study carried out in 1998. The study was designed to measure people’s reactions to their health care system. A summary of the results are shown in Table 11.6:
| Statement | Australia | Canada | N.Z. | U.K. | U.S. |
|---|---|---|---|---|---|
| Difficulties getting needed care | 15 | 20 | 18 | 15 | 28 |
| Recent changes will harm quality | 28 | 46 | 38 | 12 | 18 |
| System should be rebuilt | 30 | 23 | 32 | 14 | 33 |
| No bills not covered by insurance | 7 | 27 | 12 | 44 | 8 |
| Sample size | 1000 | 1000 | 1000 | 1000 | 1000 |
| Health care expenditure (USD per person) | 1805 | 2095 | 1352 | 1347 | 4090 |
1. We want to compare the 30% of Australians agreeing to the “System should be rebuilt” with the 23% of Canadians agreeing to the same statement; which sampling situation is appropriate, A, B or C?
Situation A is appropriate; we have two independent samples of people from different countries.
Using the percentages, the proportions of interest are \(\hat p_1 = 0.3 = \frac{300}{1000}\); \(\hat p_2 = 0.23 = \frac{230}{1000}\) (with sample sizes of 1000)
The standard error for the difference between these proportions is obtained using the formula
\[se(p_1-p_2) = \sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\] \[se(\hat p_1-\hat p_2) = \sqrt{\frac{0.30(1-0.30)}{1000}+\frac{0.23(1-0.23)}{1000}}=0.0197\]
2. The respondents could choose: ‘agree’ ‘disagree’ or ‘don’t know’ to the statements in the table above. If we compared the proportion of Canadians who agreed “Recent changes will harm quality” with those Canadians who disagreed with that statement (the percentage disagreeing was 15%), which sampling situation applies A, B or C?
Situation B is appropriate. We have one sample of Canadians who either agree or disagree with this statement.
\(\hat p_1 = \frac{460}{1000} = 0.46\); \(\hat p_2 = 0.15\)
The standard error for the difference between these proportions is obtained using the formula
\[se(p_1-p_2) =\sqrt{\frac{p_1+ p_2-(p_1-p_2)^2}{n}}\]
\[se(\hat p_1-\hat p_2) =\sqrt{\frac{0.46+ 0.15-(0.46-0.15)^2}{1000}}=0.022\]
3. If we wanted to compare the proportion of people in the U.K. agreeing to “Difficulties getting needed care” and agreeing to “System should be rebuilt” what sampling situation would apply, A, B or C?
Situation C is appropriate. The same set of people are being asked (we have one sample) and they can agree with both these statements.
\(\hat p_1 = \frac{15}{100} = 0.15\); \(\hat p_2 = \frac{14}{100} = 0.14\)
The standard error for the difference between these proportions is obtained using the formula
\[se(p_1-p_2) = \sqrt{\frac{Min(p_1 + p_2, q_1 + q_2)-(p_1-p_2)^2}{n}}\]
- \(\hat q_1 = 1 - \hat p_1 = 1 - 0.15 = 0.85\); \(\hat q_2 = 1 - \hat p_2 = 0.86\)
\[se(p_1-p_2) = \sqrt{\frac{Min(0.15 + 0.14, 0.85 + 0.86)-(0.15-0.14)^2}{1000}}\] \[se(p_1-p_2) = \sqrt{\frac{Min(0.29, 1.71)-(0.15-0.14)^2}{1000}}\]
\[= \sqrt{\frac{0.29 - (0.15-0.14)^2}{1000}} = 0.017 \]
An example of the differences between the confidence intervals calculated using the different standard error formulae for situations (A, B or C) can be seen below.
Q11.2 A survey was undertaken to ascertain the favourite film genre of undergraduates from the University of St Andrews (and only one genre could be chosen). The results were as follows: romantic comedies 13%, musicals 8%, science-fiction/fantasy 22%, romance 27%, westerns 5%, war 8%, horror 9%, other 8%. What sampling situation (i.e. A-C) best reflects this situation?
Q11.3 If, from the same survey, the proportion of first year students who like romantic comedies is compared to the proportion of second year students who like romantic comedies, what sampling situation is this?
Q11.4 If, instead of being asked to choose one favourite genre, the students can choose a number of genre they enjoy from a list, which may lead to, for example, 53% of students who said they liked romantic comedies etc. What sampling situation would this be?
11.5 Odds ratios
In this section we calculate an odds ratio (OR) to quantify the extent of the association between two groups. An odds ratio is a relative measure of effect, which allows, for example, the comparison of an intervention group of a study relative to a control, or placebo, group. Therefore they are most often used in medicine to identify potential causes of disease or ascertain the effect of a treatment.
We need first to define what are meant by statistical odds.
Note: Statistical odds are not quite the same as betting odds. Betting odds are the probability of an event taking place which allow the prospective winnings to be calculated if the event happens. Statistical odds express relative probabilities.
11.5.1 Calculating the odds of success
The odds of success are defined to be:
\[odds=\frac{p(\textrm{success})}{p(\textrm{failure})} = \frac{p}{1-p}\]
Hence, if \(p=0.8\), the odds of success are
\[odds=\frac{p}{1-p}=\frac{0.8}{1-0.8}=\frac{0.8}{0.2}=4\]
A few points to note about odds:
- Odds are never negative.
- When the odds are greater than 1, then success is more likely than failure.
- When the odds of success=4 (for example), success is four times as likely as a failure; we expect 4 successes for every one failure.
- When the odds of success is \(\frac{1}{4}=0.25\), failure is four times as likely as a success; we expect to see one success for every 4 failures.
We can rearrange the formula above to obtain the probability of success from the odds:
\[p=\frac{\textrm{odds}}{\textrm{odds+1}}\] and so if the odds is 4, then
\[p=\frac{4}{(4+1)}=\frac{4}{5}=0.8\].
11.5.2 Calculating the odds of success for 2 x 2 tables
In the wind farm example we are interested in comparing the odds of detecting at least one bird at a location in phase A compared with phase C. To calculate the odds of success in each of phase A and phase C we
view the data as a 2 x 2 table, and
calculate the odds of success for each row of this table.
| 0 | 1 | Sum | |
|---|---|---|---|
| A | 10335 | 1143 | 11478 |
| C | 5436 | 460 | 5896 |
| Sum | 15771 | 1603 | 17374 |
For the phase A (first row) we start by finding the sighting probability:
\[\hat p_A=\frac{1143}{1.1478\times 10^{4}}=0.1\]
and from there we can find the odds of success:
\[\textrm{odds}_A =\frac{\hat p_A}{(1-\hat p_A)}=\frac{0.1}{(1 - 0.1)}= 0.111\]
The odds for phase A are less than 1 which means that the probability of detecting a bird is much lower than the probability of not detecting a bird:
- failure (absence) is more likely than success (presence).
We perform the same calculations for phase C. The probability of a bird is:
\[\hat p_C=\frac{460}{5896}=0.078\]
The odds of success is:
\[\textrm{odds}_C = \frac{\hat p_C}{(1-\hat p_C)}= 0.084621\]
The odds for phase C are also less than 1 which means that the probability of bird presence is much lower than the probability of bird absence.
- failure (absence) is more likely than success (failure).
11.5.3 Calculating the odds ratio
The relevant odds known, the odds ratio can then be calculated:
the numerator is the odds in the intervention arm/group 1
the denominator is the odds in the control arm/group 2
If the outcome is the same in both groups, the ratio will be 1: this implies there is no difference between the two arms (groups) of the study.
However:
if the OR is \(> 1\) the intervention is better than the control.
if the OR is \(< 1\) the control is better than the intervention.
For example, in the wind farm data, the two groups could be the presence (or absence) of animals seen A and C the wind farm development.
So in the medical study of TEON, we might be interested in the presence, or absence, of blindness in people who are either Vitamin D deficient or have acceptable Vitamin D levels.
Whatever the situation, we must calculate the odds of success for each of the two groups.
We can find the ratio of these two values (a so-called odds ratio).
- We do this following the procedure stated earlier, the ‘intervention’ is the numerator:
\[\theta=\frac{\text{odds}_C}{\text{odds}_A}=\frac{\hat{p}_C/(1-\hat{p}_C)}{\hat{p}_A/(1-\hat{p}_A)}=\frac{(460 / 5896) / (1-(460/ 5896))}{(1143 / 1.1478\times 10^{4}) / (1-(1143 / 1.1478\times 10^{4})}= 0.085/ 0.111= 0.765\]
Remember:
If the OR is \(> 1\) the intervention is better than the control.
If the OR is \(< 1\) the control is better than the intervention.
In our example, the OR is \(<1\) so the odds of seeing something in phase C (intervention group) is lower than the odds of seeing something in phase A (control group) as this ratio is less than 1.
- If the reverse was true, the odds ratio (\(\theta\)) would be greater than 1 but can never be zero or negative.
11.5.4 Confidence intervals for odds ratios
While the odds ratio calculated above is based on our sample estimates for the two proportions, and thus constitutes our `best guess’ for the odds ratio (\(\hat{\theta}\)), this value will change from survey to survey and so it is often useful to construct a 95% confidence interval for the odds ratio.
Previously we have used the normal and \(t\)-distributions to construct confidence intervals, however, these are poor choices to use for confidence intervals based around the odds ratio because, unless the sample size is large, the sampling distribution for the odds ratio (\(\theta\)) is highly skewed.
For example, even if the true, and unknown, odds ratio is 1 the estimate cannot be much smaller (since it can never be zero or negative) but it can often be much higher just due to chance.
This means the estimates are not guaranteed to be symmetrically distributed about the true odds ratio.
For this reason, the log of the odds ratio is used as the centre of the associated confidence intervals since these estimates tend to be more symmetrical.
Specifically, the log of the odds ratio estimates tend to be approximately normal with a mean of \(\log(\theta)\) and a standard error of:
\[se_{OR}=\sqrt{\frac{1}{n_{11}}+\frac{1}{n_{12}}+\frac{1}{n_{21}}+\frac{1}{n_{22}}}\]
where \(n_{11}...n_{22}\) are based on the number of observations in each group/outcome category.
We can construct the 95% confidence interval for \(\log\theta\) using the estimate for \(\log\hat{\theta}\). We can then get values back on the raw odds ratio scale by ‘undoing’ this log function using the exponential function.
For example, if we apply the log function to the value of 2 we get: log(2)=0.693
and we can undo this function by applying the exponential function: exp(0.693)=2.
A large-sample, confidence interval for log of the odds ratio can be found using:
\[\log(\hat{\theta}) \pm z_{1-\alpha/2} \times se_{OR}\]
we can then exponentiate the upper and lower limits of this interval to obtain a confidence interval for the odds ratio.
Example Back to our wind farm example, entries from the centre of the following table provide the numbers of observations, \(n_{11}\) etc.:
| 0 | 1 | Sum | |
|---|---|---|---|
| A | 10335 | 1143 | 11478 |
| C | 5436 | 460 | 5896 |
| Sum | 15771 | 1603 | 17374 |
So in this case, comparing phases A and C means these values are:
- the value for row 1 of interest in the table and in column 1: \(n_{11}=10335\)
- the value for row 1 of interest in the table and in column 2: \(n_{12}=1143\)
- the value for row 2 of interest in the table and in column 1: \(n_{21}=5436\)
- the value for row 2 of interest in the table and in column 2: \(n_{21}=460\)
Therefore, the standard error of the odds ratio is:
\[se_{OR}=\sqrt{\frac{1}{1.0335\times 10^{4}}+\frac{1}{1143}+\frac{1}{5436}+\frac{1}{460}}=0.058\]
- As is typical, the standard error decreases as the cell counts increase. For instance, if all cell entries were 10,000 the new \(se_{OR}\) would be just 0.02.
In our example, the estimated odds ratio is: 0.765 and we are interested in whether this could be a 1:1 ratio and therefore even odds. A 95% confidence interval for this ratio is:
\[\log(0.765) \pm 1.960 \times 0.058\]
which returns a lower limit of -0.381 and an upper limit of -0.155.
These upper and lower limits are exponentiated:
\[\big(\text{exp}(-0.381), \text{exp}(-0.155)\big)\] to give
This result tells us that an odds ratio value of 1 is not a plausible value for the odds and so the odds in phase A appear to be genuinely higher than in phase C.
Additionally, with 95% confidence we estimate the odds of presence of a bird in phase A compared with phase C appears to be somewhere between 0.683 and 0.857.
11.5.4.1 Doing this in R
The package epitools - epidemiology tools (Aragon 2020) is used for calculating odds ratios.
# Create object containing the number of successes (presence) and failures (absence)
counts <- c(1143, 10335, 460, 5436)
# Convert to a matrix
matcounts <- matrix(counts, nrow=2, byrow=TRUE)
# Add row and column names
dimnames(matcounts) <- list("Phase"=c("A","C"), "AnimalsSeen"=c("Presence","Absence"))
matcounts AnimalsSeen
Phase Presence Absence
A 1143 10335
C 460 5436# Load package
require(epitools)
# Odds ratio and CI
OR <- oddsratio(matcounts, method='wald', rev='rows')
# Print out odds ratio and CI
OR$measure odds ratio with 95% C.I.
Phase estimate lower upper
C 1.000000 NA NA
A 0.765143 0.6833239 0.856759rev='rows'reverses the rows in the data object because we want the odds ratio to be odds\(_C\)/odds\(_A\).method='wald'there are several method for calculating CI. Wald’s method uses the normal approximation as described above.
11.5.5 Final note on odds ratios
The survey example given above would not typically be analysed using odds ratios in real life. Odds ratios are typically employed in case control studies where a typically (rare) disease is being investigated. These studies tend to be retrospective in that ‘cases’ are found (with the disease) and then ‘controls’ and the initial circumstances of the cases and controls are compared(Lewallen and Courtright 1998). Controls are created such that they are matched, in some way, to cases, for example by age, sex, smoker etc. The matching factor is not the variable of interest; if it is, it should not be used as a matching criterion.
Example A mixed sex group (40 male, 40 female) of patients with a disease X are documented. Another 40 control (without the disease) individuals are matched for age and sex. The numbers with known exposure to, for example, asbestos in each group is determined (see table below).
| Disease | No disease | Sum | |
|---|---|---|---|
| Asbestos | 31 | 1 | 32 |
| No asbestos | 9 | 39 | 48 |
| Sum | 40 | 40 | 80 |
Hence the proportions with and without exposure to asbestos in each group can be obtained.
\[Pr(\textrm{Asbestos|Disease}) = \frac{31}{40} = 0.775\]
\[Pr(\textrm{Asbestos|No disease}) = \frac{1}{40} = 0.025\]
\[Pr(\textrm{No Asbestos|Disease}) = \frac{9}{40} = 0.225\]
\[Pr(\textrm{No Asbestos|No disease}) = \frac{39}{40} = 0.975\]
Therefore, the odds of exposure to asbestos for the disease group are:
\[\textrm{Odds}_{\textrm{Disease}} = \frac{Pr(\textrm{Asbestos|Disease})}{Pr(\textrm{Asbestos|No disease})} = \frac{0.775}{0.225} = 3.444\]
and for the control group:
\[\textrm{Odds}_{\textrm{No disease}} = \frac{0.025}{0.975} = 0.026\]
Hence, the odds ratio is
\[\textrm{Odds ratio} = \frac{3.444}{0.026} = 134.333\]
Confidence intervals can be created as before: \[\log(134.333)\pm 1.959964 \times \sqrt{\frac{1}{31}+\frac{1}{1}+\frac{1}{9}+\frac{1}{39}}\]
\[4.9 \pm 1.959964 \times 1.081\]
resulting in values of 2.7812 and 7.0195 which, exponentiated, gives a 95% confidence interval of (16.1, 1118.2) - clear evidence of an association between asbestos and the disease.
These calculations can easily be done in R.
matrixasbestos <- matrix (c(1,31,39,9), nrow=2, ncol=2, byrow=T)
###note order changed of variables
OR <- oddsratio(matrixasbestos, method='wald', rev='rows')
# Print out odds ratio and CI
OR$measure odds ratio with 95% C.I.
Predictor estimate lower upper
Exposed2 1.0000 NA NA
Exposed1 134.3333 16.13831 1118.174Q11.5 Imagine a case-control study looking at the relationship between male pattern baldness and prostate cancer: 101 males with prostate cancer were assessed for the presence or absence of substantial male pattern baldness; 49 were assessed as bald. The control group (n = 98) did not have cancer and 80 were characterised as bald. The question of interest here, is whether baldness predicts prostate cancer? Note that this is NOT an independent sample of counts because the two groups (cancer or no cancer) have been matched in some way (possibly age for example).
| Cancer | No cancer | Sum | |
|---|---|---|---|
| Bald | 49 | 80 | 129 |
| No bald | 52 | 18 | 70 |
| Sum | 101 | 98 | 199 |
Using the above table, calculate the probability of being bald given cancer (i.e. \(Pr(\textrm{bald|cancer})\) and the probability of being bald given no cancer.
Q11.6 What about the probability of cancer given baldness and the probability of cancer given no baldness? Is it legitimate to compare these proportions? Hint: think about the independence of individuals within the groups being compared.
Q11.7 What method (direct comparison of proportions or odds ratios) would you use to analyse these data and why?
11.6 Summary
Proportions are often incorrectly treated in the scientific literature so it is useful to know how to handle such statistics. There are other ways to handle cross classified count data. One of which we will consider in the material on \(\chi^{2}\) test.
11.6.1 Learning outcomes
At the end of this chapter you should be able to:
- recognise that a problem involves proportions,
- construct an appropriate confidence interval for a proportion and a difference between proportions,
- construct a significance test testing the difference between proportions, and
- have a basic understanding of odds ratios.
11.7 Answers
Q11.1 There are certainly two outcomes for each trial (seen or not seen). Within a phase we can assume there is the same probability of success. There are fixed number of trials (sampling localities) but they may not be independent as sampling locations close to each other may have similar characteristics.
Q11.2 This is sampling situation B, one sample with several mutually exclusive categories, i.e. there is one sample of students and they chose one from many categories of films.
Q11.3 This is sampling situation A, two independent samples; one of first years and the other second years.
Q11.4 This is sampling situation C, one sample with many ‘yes/no’ items, i.e. there is one sample of students and for each film genre listed, they indicate whether they enjoy the genre or not.
Q11.5 The \(Pr(\textrm{Bald|Cancer})\) = 49/101 and \(Pr(\textrm{Bald|No Cancer})\) = 80/98 (although presumably no one is too concerned about male pattern baldness given a diagnosis of cancer!).
Q11.6 The \(Pr(\textrm{Cancer|Bald})\) = 49/129 and \(Pr(\textrm{Cancer|Not bald})\) = 52/70 are the statistics of interest. In the previous question the two groups being compared were ‘Cancer’ and ‘No cancer’; individuals were allocated to each of these groups based on their prognosis. In this question, the two groups being compared are ‘Bald’ and ‘Not bald.’ The two proportions cannot be legitimately compared because individuals within the two groups have been matched in some way; for example, there are 129 subjects classed as bald, but this group consists of subjects (with and without cancer) and these individuals have been matched in some way (i.e. they have similar characteristics) and are therefore not independent.
Q11.7 The control group does not reflect the occurrence of cancer in the general population (because they have been chosen by virtue of not having cancer) and so there would be no value in directly comparing the probabilities anyway. However, the odds ratio does allow us to explore the relative odds of getting cancer.