Chapter 7 Confidence intervals for sample means
… a hypothesis test tells us whether the observed data are consistent with the null hypothesis, and a confidence interval tells us which hypotheses are consistent with the data.
William C. Blackwelder.
7.1 Introduction
We would like a sample to be representative of the target population. If we were to generate several samples from the same population and then calculate the sample statistics for each sample (e.g. a mean), it is likely that the statistics would differ between samples - this is due to sampling error and is unavoidable. However, the extent to which these sample means will vary is somewhat predictable and we can use this information to provide a measure of uncertainty for the sample statistic. This takes the form of an interval between which we have some confidence that the true mean lies - this is called a confidence interval (CI). There are several methods which can be used to obtain a CI, depending on whether the data fulfill various criteria.
In this chapter you will:
- examine the behaviour of the sample mean
- quantify the precision of the sample mean and hence calculate a confidence interval,
- quantify the precision of the difference between two sample means and again calculate a confidence interval, and finally
- consider an alternative approach for obtaining a confidence interval.
In this chapter we are mainly concerned with sample means but similar uncertainty will exist for other sample statistics such as the median, variance and proportions. In the final section we consider how the uncertainty of these other statistics can be quantified.
7.2 Uncertainty of the sample mean
To illustrate the variability in the sample, we consider the distribution of womens heights. Assume that height is normally distributed with a mean of 160 cm and a standard deviation of 6 cm, i.e. Height \(\sim N(\mu=160, \sigma^2=6^2)\).
If we randomly draw five values from this distribution, then these might be: 152.7, 161.7, 166.6, 145.9 and 162.6
The mean of this sample is 157.9 cm and this is quite close to the population mean. Usually however, we don’t know the population mean and so, in general, we want to know how well a sample mean represents the population. To find out how good an estimate is, we need to know how precise it is and this depends on:
- the sample size, and
- the variability in the population.
Intuitively, we might expect that if the population is very variable, then the distribution of sample means may also be variable. Conversely, if the population is not very variable, then we might expect that sample means will be similar to the population mean and also to each other. In addition, a large sample may more closely resemble the population than a small sample and, hence, the sample mean from a large sample may be more similar to the population mean than the sample mean from a small sample.
This concept can be illustrated by generating many samples from a known population, calculating the mean for each sample and looking at the distribution of the sample means. In Figure (7.1), 1000 sample means have been generated from samples of different sizes, drawn from a normal distribution with mean 160 and standard deviation 6.
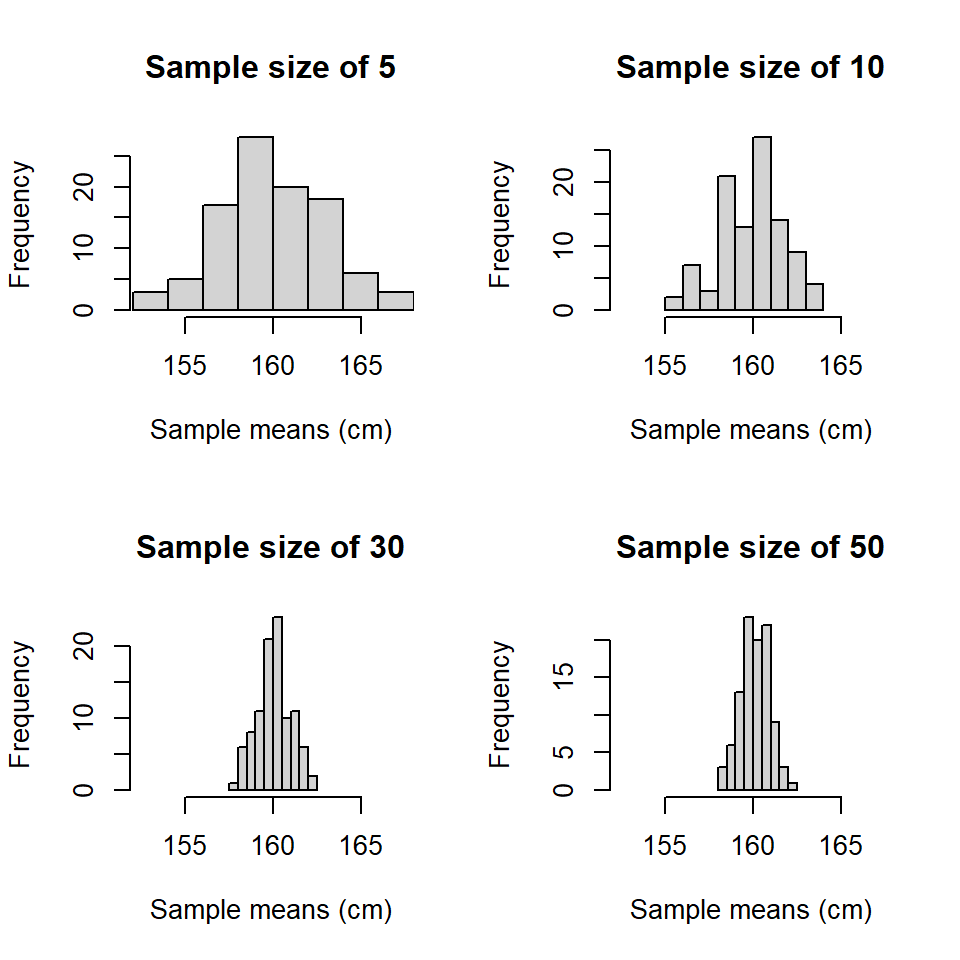
Figure 7.1: Distributions of 1000 sample means using four different sizes of sample. The underlying population was \(N(160,6^2)\).
There are two things to notice about these distributions of sample means:
- the distributions are centered about the true population mean of 160, and
- the sample means range from about 152 to 168 when the sample size is 5, but this spread reduces as the sample size increases.
These patterns will be similar for any distribution of sample estimates and so can be used to inform how precise a sample mean might be.
7.2.1 Precision of the sample mean
The standard deviation of the sample means is found by dividing the population standard deviation by the square root of the sample size being averaged:
\[sd(\textrm{sample mean}) = \frac{\textrm{Population SD}}{\sqrt{\textrm{sample size}}}\]
The standard deviation of a sampling distribution is called a standard error. Therefore, substituting the usual notation (see Chapter 3) into this formula, the standard error of the mean is given by:
\[se(\hat \mu) = \frac{\sigma}{\sqrt{n}}\]
Thus, using the height data, the standard error for a sample size of 5 is given by:
\[se(\hat \mu) = \frac{6}{\sqrt{5}} = 2.68\]
As shown in Figure 7.1, the standard deviation (and hence standard error) of the distribution of the sample mean reduces as the sample size increases; the standard error using a sample size of 30 is
\[se(\hat \mu) = \frac{6}{\sqrt{30}} = 1.095\]
7.2.2 Confidence interval with known \(\sigma\)
In this example, we assumed the data were normally distributed and, as we have seen in Figure 7.1, the distributions of the sample mean were also normally distributed. This is very handy because we know that for any normally distributed variable, 95% of the time a randomly chosen value will fall within 1.96 standard deviations of the mean. Hence, the sample mean will fall within 1.96 standard deviations of the true population mean about 95% of the time (or for about 95% of samples taken). While we rarely know the true population mean, it is likely that the estimate of the sample mean will fall within about 1.96 standard deviations of the population mean. Thus, we can derive an upper and lower limit between which we think the true population mean will lie - this is called a confidence interval. A 95% confidence interval for the sample mean is given by the following:
\[ \hat \mu - 1.96 \times \frac{\sigma}{\sqrt{n}} \quad ; \quad \hat \mu + 1.96 \times \frac{\sigma}{\sqrt{n}}\] or, writing this more succinctly as,
\[ \hat \mu \pm 1.96 \times \frac{\sigma}{\sqrt{n}}\]
Thus, for a sample of size 5, the 95% confidence interval for the mean will be
\[157.9 \pm 1.96 \times 2.68\]
\[157.9 \pm 5.25\]
which results in the limits 152.6 cm and 163.2 cm. We can see for a distribution with a mean and variance equal to our sample mean and standard deviation i.e. \(N(\mu=157.9, \sigma^2=2.68^2)\), that 95% of the distribution lies between these limits (Figure 7.2). This means that if we repeatedly take samples of size 5, calculate the sample mean and a 95% CI for the mean, 95% of the confidence intervals will include the true population mean.
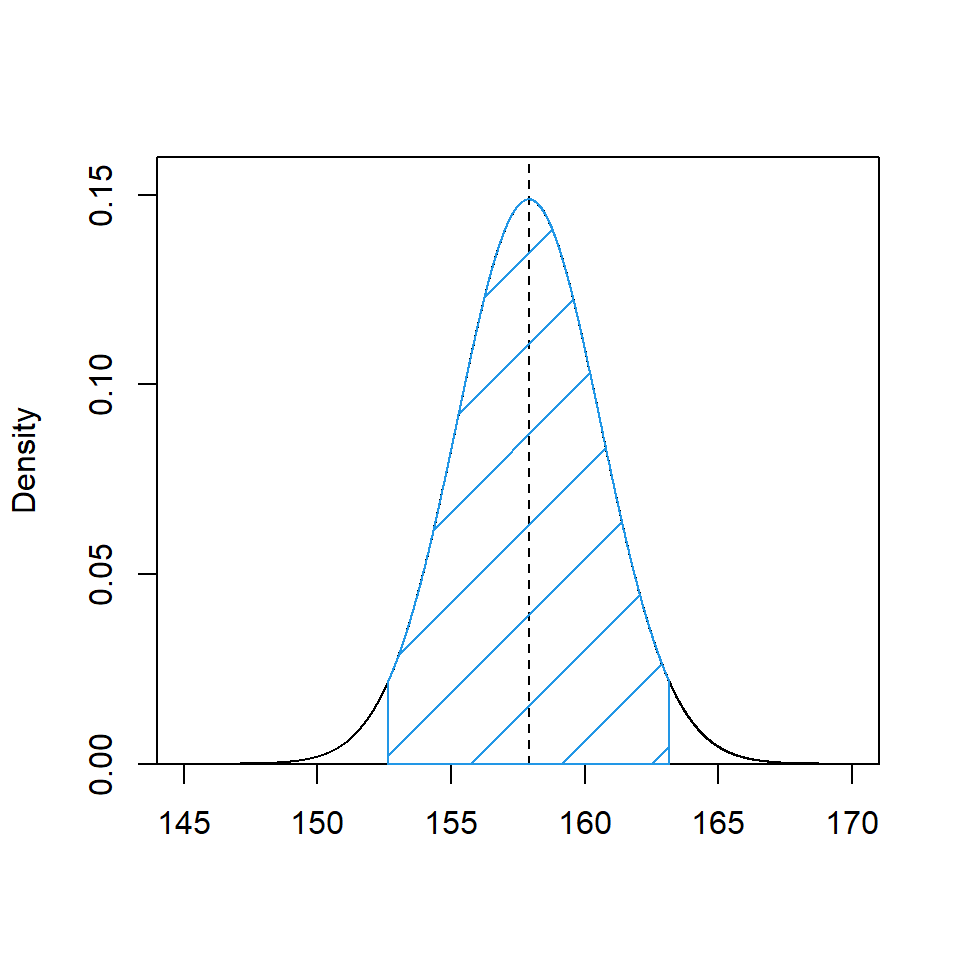
Figure 7.2: Sampling distribution of the sample mean for a sample of size 5. 95% of the central part of the distribution is shaded blue. The sample mean is shown by the dotted line.
We can think of 1.96 as a value which multiplies the standard error to provide a value above and below the sample mean to create the confidence interval. Increasing or decreasing this multiplier will result in wider and narrower intervals and we look at this later. Before that we consider a fundamental theorem in statistics.
To illustrate a confidence interval we used data from a normal distribution and, in general, we don’t usually know if the data are drawn from a normal distribution! However, help is at hand in the form of the Central Limit Theorem.
7.2.2.1 Central limit theorem
The Central Limit Theorem (CLT) states that no matter what distribution we sample from, the distribution of the sample means (\(\hat \mu\)) is closely approximated by the normal distribution in large samples.
We can see this in Figure 7.1, but how large a sample is required for reliable estimation of the population mean? The sample size required depends somewhat on the data: for data from symmetrical distributions a sample of 5 may be sufficient; for heavily skewed data a sample of 50 may be required.
In calculating a CI, we also need to consider the variability in the data and this is quantified by the standard deviation. In the example above, we knew the population standard deviation but what happens if we don’t know the population standard deviation? We consider this next.
7.2.3 Confidence interval with unknown \(\sigma\)
If the population standard deviation is unknown (and in fact the population standard deviation is rarely known), the population standard deviation (\(\sigma\)) is simply replaced by the sample standard deviation (\(s\)) in the formula for the standard error:
\[se(\hat \mu)=\frac{\textrm{sample SD}}{\sqrt{\textrm{sample size}}} = \frac{s}{\sqrt{n}}\]
Thus, for the sample of five heights, the sample standard deviation is 8.415 and so the sample standard error is
\[se(\hat \mu) = \frac{8.415}{\sqrt{5}} = 3.763\]
When we sample data from a normal distribution and we know the population standard deviation (\(\sigma\)), the distribution of sample means is exactly normally distributed about the true population mean, \(\mu\). When we don’t know the population standard deviation, we introduce a new source of variability because we use the sample standard deviation of the data instead of a known population standard deviation. Therefore, rather than using quantiles from the normal distribution to find the multipliers needed to calculate the confidence interval, we use a different distribution; the \(t\) distribution is used to find the multiplier. Before continuing with the calculation we look at the \(t\) distribution and see how it compares to a standard normal distribution.
7.2.3.1 The \(t\) distribution
The \(t\) distribution (also known as Student’s \(t\) distribution) is symmetrical about zero and has a similar shape to the standard normal distribution. However, rather than being defined by a mean and variance, the \(t\) distribution is indexed by a parameter called the degrees of freedom (\(df\)) (i.e. \(t_{df}\)). The degrees of freedom are determined by the sample size such that \(df=n-1\). When \(n\) is small the \(t\) distribution has fatter tails and a flatter top compared with the normal distribution; as \(n\) (and thus \(df\)) increases, the \(t\) distribution become more and more like a standard normal distribution (Figure 7.3). As an example, when \(n=11\), and hence \(t_{df=10}\), only 92% of the distribution falls within 1.96 standard deviations either side the mean, whereas for a standard normal distribution, 95% of the distribution falls within 1.96 standard deviations of the mean. For a \(t_{df=10}\) distribution, 95% of the distribution will lie between 2.23 standard deviations of the mean.
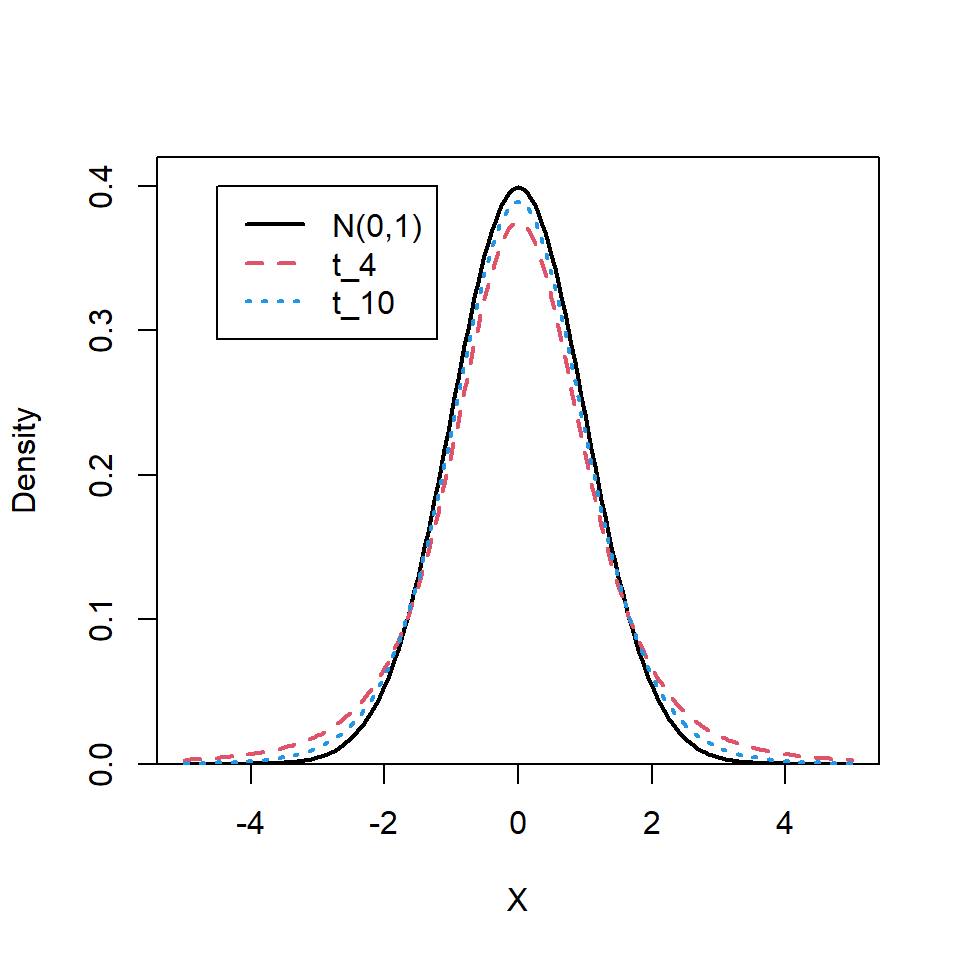
Figure 7.3: Comparison of standard normal and \(t\) distributions with 4 and 10 \(df\).
7.2.3.2 Confidence interval for the sample mean
When the population standard deviation is unknown and estimated by the sample standard deviation, the multiplier is found from the \(t\) distribution such that the confidence interval limits are found from
\[\hat{\mu} - t_{(1-(\alpha/2), df=n-1)} \times \frac{s}{\sqrt{n}} \quad;\quad \hat{\mu} + t_{(1-(\alpha/2), df=n-1)} \times \frac{s}{\sqrt{n}}\] or more succinctly,
\[\hat{\mu}\pm t_{(1-(\alpha/2), df=n-1)}se(\hat{\mu})\]
where \(t_{(1-\alpha/2, df=n-1)}\) represents a value (multiplier) from the \(t_{df=(n-1)}\) distribution; this indicates how far we need to extend either side of the sample estimate in order to ‘catch’ the true mean with some associated confidence, represented by \(\alpha\). The confidence represents how confident we want to be that the interval contains the true mean.
The most frequently quoted CI are 95% confidence intervals (i.e. we want to be 95% confident that the interval contains the true mean). For 95% CI, \(\alpha = 5\)%, thus \(1 - \frac{\alpha}{2} = 1 - \frac{0.05}{2} = 0.975\). Thus, the multiplier is the quantile \(q\) such that \(Pr(X \le q) = 0.975\) where \(X \sim t_{{df}}\).
To illustrate how to find the multiplier, let’s return to the height sample data. Figure @ref(fig:tdist.ca) shows that a \(Pr(X \le 2.78) = 0.975\) and because the \(t\) distribution is symmetric round zero, we know that \(Pr(X \le -2.78) = 0.025\), hence 95% of the area (the red shaded area) will lie between -2.78 and 2.78 where \(df=4\).
(ref:tdist.ca) Probability density distribution for \(t_{df=4}\). The red shaded area is 95% of the area with 2.5% in each tail.
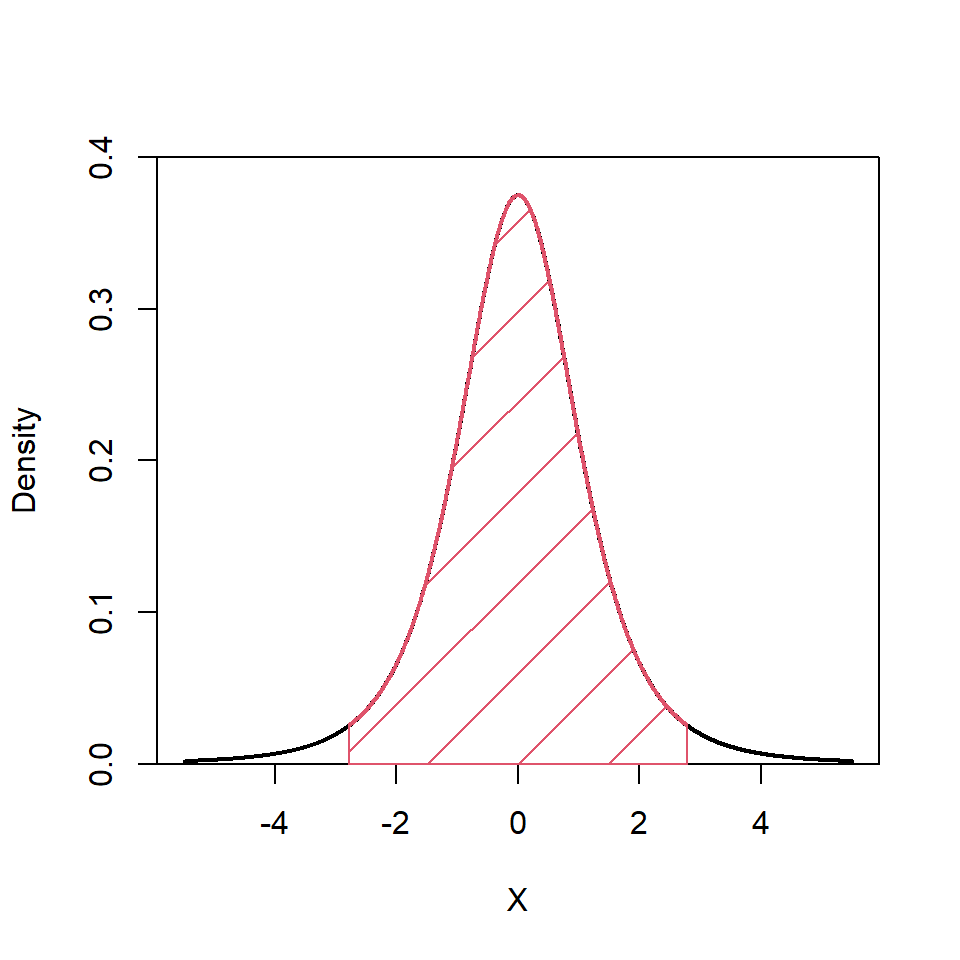
(#fig:tdist.ca)(ref:tdist.ca)
Thus using the sample standard deviation, the interval is found from:
\[157.9 \pm t_{0.975, \textrm{df}=4} \times 3.763\]
and substituting in the value for the \(t\)-multiplier, \(t_{0.975, \textrm{df}=4} = 2.78\), gives
\[157.9 \pm 2.78 \times 3.763\] \[157.9 \pm 10.46\]
Thus, the 95% confidence interval for the mean is 147.4 to 168.4 cm; 95% of the time the true mean will lie in the range 147.4 and 168.4 cm. This is wider than the confidence interval found using the population standard deviation (which was 152.6 to 163.2 cm) because of the additional uncertainty about the variability of the distribution.
7.2.3.3 What does confidence mean?
Confidence is a long run process, it does not apply to any one particular interval. Essentially, if we repeatedly take samples from a population and calculate a 95% CI (just as we have done above for one sample), 95% of the intervals will contain the true population mean. That means 5% of the intervals will not contain the true mean!
If we wanted to increase the chance of catching the true mean, the interval could be widened by considering 99% confidence intervals. In this case for our sample of five heights, the \(t\)-multiplier would be 4.6 resulting in an interval of 140.6 to 175.2 cm. Conversely, a 90% confidence interval would be narrower i.e. (149.9 to 165.9 cm). Both 90% and 99% confidence intervals are used but 95% CI are the ones most frequently stated.
7.2.3.4 Doing this in R
To start with, we illustrate how to calculate a confidence interval by obtaining all the individual components. The \(t\)-multiplier is found from the cumulative distribution function for the \(t\) distribution qt - this is similar to the qnorm function introduced in Chapter 6.
# 95% CI for the sample mean assuming underlying population is normal
# Create object for sample data
hgt <- c(152.7, 161.7, 166.6, 145.9, 162.6)
# Save the individual components of the CI
# Sample mean
mean.hgt <- mean(hgt)
mean.hgt[1] 157.9# Sample standard deviation
sd.hgt <- sd(hgt)
sd.hgt[1] 8.415165# Number of observations
n <- length(hgt)
n[1] 5# Calculate standard error
se.hgt <- sd.hgt/sqrt(n)
se.hgt[1] 3.763376# t-multiplier for 95% CI
tmult <- qt(p=0.975, df=4)
tmult[1] 2.776445# Lower limit
mean.hgt - (tmult*se.hgt)[1] 147.4512# Upper limit
mean.hgt + (tmult*se.hgt)[1] 168.3488The above commands illustrate how to construct the confidence intervals from the individual components. However, there is a short cut (isn’t there always in R) to obtain a CI. We make use of the t.test function; the t.test function does a lot more than provide confidence intervals (which we will explore in the following chapter) but for now we only want the CI which are given by specifying $conf.int.
# 95% CI (default)
t.test(x=hgt)$conf.int[1] 147.4512 168.3488
attr(,"conf.level")
[1] 0.95# 90% CI
t.test(x=hgt, conf.level=0.90)$conf.int[1] 149.8771 165.9229
attr(,"conf.level")
[1] 0.9# 99% CI
t.test(x=hgt, conf.level=0.99)$conf.int[1] 140.5731 175.2269
attr(,"conf.level")
[1] 0.99Q7.1 A researcher was interested in the typical size of trees (measured as diameter at breast height, dbh) of a particular species in a forest. Data on dbh (in cm) had been collected on a sample of 50 trees. The mean dbh was 15.3 cm and the standard deviation was 30 cm.
a. What is the standard error of the mean?
b. Which of the following multipliers should be used for a 90% confidence interval?
qt(p=0.90, df=49)[1] 1.299069qnorm(0.05)[1] -1.644854qt(p=0.95, df=49)[1] 1.676551qt(p=0.975, df=49)[1] 2.009575c. Calculate a 90% confidence interval for the mean.
d. Interpret the confidence interval.
Q7.2 A study of birth weight was conducted in San Francisco, US. The summary statistics of weights of babies for the group of non-smoking mothers are as follows: \(n=742\), \(\hat \mu = 123.05\) ounces and \(s = 17.4\) ounces. Calculate a 95% confidence interval for the mean; the sample size is large and so assume that the \(t\) multiplier is 1.96. The full data set can be found here.
7.3 Difference between two group means
Sometimes we want to compare two means, for example the mean blood pressure of patients that have received one of two treatments or the mean yield of tomato plants grown in one of two varieties of potting compost. Hence, we are interested in the difference between the two means and want to find a confidence interval for the difference. The process is very similar to that described previously.
Assume we have two groups, which we call \(A\) and \(B\), and sample means have been obtained, \(\hat \mu_A\) and \(\hat \mu_B\). The difference between the sample means is simply given by
\[\textrm{difference } A - B = \hat \mu_A - \hat \mu_B\]
If this difference is zero (or very close to zero), then it likely that there is no real difference between these two groups. However, if it is not zero there are two possible alternatives:
- the two samples are from the same parent population and the difference is due to sampling variability, or
- the two samples are from different populations and so there is a difference beyond any sampling variability.
The phrase ‘different populations’ is used here to refer to parent populations that have different population means, however, we also need to consider whether the parent populations have different standard deviations; as we shall see, this is taken account of when considering the precision of the estimate of the difference.
In the next chapter we look at formal statistical tests to determine between the two alternatives described above but here we want to find an interval around the estimate of the difference that we are confident (to some level) contains the true difference.
The confidence interval for the difference in the means is given by:
\[(\hat \mu_A - \hat \mu_B) \pm t_{(1-(\alpha/2), n-1)}se(\hat \mu_A - \hat \mu_B)\]
where \(se(\hat \mu_A - \hat \mu_B)\) is the standard error of the difference.
The standard error of the difference is obtained by combining the uncertainty of the two sample estimates and the calculation depends on whether the variability of the two groups can be assumed to be the same (or very similar) or not.
Q7.3 According to an advertising campaign, batteries from brand \(A\) last longer than batteries from brand \(B\). In order to compare the two brands we select a random sample of 90 brand \(A\) batteries and 60 brand \(B\) batteries. The sample of brand \(A\) batteries run continuously for a total of 4451 minutes with a sample standard deviation of 6.32 minutes. The sample of brand \(B\) batteries run continuously for a total of 2763 minutes with a sample standard deviation of 3.31 minutes. Assume that the data are normally distributed.
Find estimates for \(\hat \mu_A\) and \(\hat \mu_B\), the mean running time of a battery from brand \(A\) and brand \(B\), respectively. Hence find an estimate for the difference in mean running time between the two brands.
7.3.1 Assuming equal standard deviations of the two groups
If we can assume that the two groups have the same variability, we pool the information on variability (quantified by the sample standard deviations) to generate an estimate of the pooled variability.
The standard error of the difference in sample means is the pooled estimate of the common standard deviation (\(s_p\)) (assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples,
\[se(\hat{\mu_A} - \hat{\mu_B})=s_p\sqrt{\frac{1}{n_A} + \frac{1}{n_B}}\]
where \(s_p\) is the pooled standard deviation and is found as follows:
\[ s_p = \sqrt{\frac{(n_A-1)s_A^2 + (n_B-1)s_B^2}{n_A + n_B -2}}\] The pooled degrees of freedom are given by \(df=(n_A + n_B - 2)\). These degrees of freedom are then used to find the multiplier \(t_{(1-(\alpha/2), df)}\).
This specification for the standard error and degrees of freedom are only appropriate when the two groups have equal standard deviations.
Example We continue to look at data collected from the observational study of birth weights introduced in Q7.2. In total, 1236 women were enrolled in the study and the participants came from a wide range of economic, social and educational backgrounds. We want to calculate a 95% confidence interval for the difference between the means for the mothers who smoked and mothers who did not smoke. The summary data are provided in Table 7.1.
| Smoking | n | Mean | SD |
|---|---|---|---|
| No | 742 | 123.05 | 17.4 |
| Yes | 484 | 114.11 | 18.1 |
The estimate for the difference between the non-smoking group (\(N\)) and the smoking group (\(S\)) is given by
\[\hat \mu_N - \hat \mu_S = 123.05 - 114.11 = 8.94\]
In this example, the sample standard deviations are very similar and so we will calculate the pooled standard deviation:
\[ s_p = \sqrt{\frac{(n_N-1)s_N^2 + (n_S-1)s_S^2}{n_N + n_S -2}}\] Substituting in the values gives:
\[ s_p = \sqrt{\frac{(742-1)17.4^2 + (484-1)18.1^2}{742 + 484 -2}} = \sqrt{\frac{382580.8}{1224}} = 17.68\] Thus, the standard error is
\[se(\hat{\mu}_N - \hat{\mu}_S)=s_p\sqrt{\frac{1}{n_N} + \frac{1}{n_S}} = 17.68 \sqrt{\frac{1}{742} + \frac{1}{484}} = 1.033\]
The degrees of freedom are
\[df = 742 + 484 - 2 = 1224\]
The next component of the confidence interval is the multiplier \(t_{(1-\frac{\alpha}{2}, df)}\). For a 95% confidence interval, \(\alpha=0.05\) and so we want the quantile associated with \(t_{(0.975,df=1224)}\). The degrees of freedom are large and so the relevant \(t\) distribution will be very similar to the normal distribution; the actual value of the multiplier is 1.9619. Thus the 95% confidence interval is given by
\[8.94 \pm 1.9619 \times 1.033 \]
\[8.94 \pm 2.027\]
which results in an interval 6.91 to 10.97 ounces. This interval indicates that we can be 95% confident that, on average, a baby with a non-smoking mother is likely to be about 7 to 11 ounces heavier than a baby with a mother who smokes.
7.3.1.1 Doing this in R
Again we can call on the t.test function to calculate a CI for the difference between two sample means. In the code below, the birth weights for non-smokers and smokers have been stored in objects called grpN and grpS, respectively.
# 95% CI
t.test(x=grpN, y=grpS, var.equal=TRUE)$conf.int[1] 6.911199 10.964133
attr(,"conf.level")
[1] 0.95Q7.4 For the details of battery running times provided in Q7.3, calculate the standard error (assuming the standard deviations are equal) for the difference in mean running time and hence, using the following information, calculate a 95% confidence interval for the difference in means.
qt(p=0.975, df=148)[1] 1.9761227.3.2 Assuming unequal standard deviations of the two groups
If the standard deviations of the two groups cannot be assumed to be equal, then to accurately describe the differences we need to alter the standard error and degrees of freedom calculations. This standard error formula is:
\[se(\hat{\mu}_A - \hat{\mu}_B)= \sqrt{\frac{{s_A}^2}{{n_A}} + \frac{{s_B}^2}{{n_B}}}\]
To calculate the degrees of freedom when doing the calculation by hand, use the minimum value out of \(n_A-1\) and \(n_B -1\):
\[df = Min(n_A-1, n_B -1)\]
In computing packages, the more exact (but also more tricky to calculate by hand) Welch-Satterthwaite equation is used:
\[df_w = \frac{\left(\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B}\right)^2}{\frac{s_A^4}{n_A^2(n_A-1)} + \frac{s_A^4}{n_A^2(n_A-1)}}\]
The Welch-Satterthwaite approximation for df (\(df_w\)) is always smaller than the degrees of freedom under equal standard deviation, so for the same \(\alpha\) level, the multiplier will be wider. We will investigate the effects of using this more exact formula further in the computer practical associated with this chapter.
Example Using the summary data in Table 7.1, we calculate the 95% confidence interval for the difference in means using the standard error formula that should be used if we cannot assume that the standard deviations of the two groups are the same.
The standard error formula, assuming that the standard deviations of the two groups are not equal is:
\[se(\hat{\mu}_N - \hat{\mu}_S)= \sqrt{\frac{{s_N}^2}{{n_N}} + \frac{{s_S}^2}{{n_S}}} = \sqrt{\frac{17.4^2}{742} + \frac{18.1^2}{484}} = 1.04\]
Since we are doing this calculation by hand the following formula is used to obtain the degrees of freedom.
\[df = Min(742-1, 484-1) = 483\] This results in a multiplier of 1.965, thus, the 95% confidence is given by
\[8.94 \pm 1.965 \times 1.04\] which results in an interval (6.90, 10.98), hence we can be 95% confident that the difference in birth weights between the smoking and non-smoking mothers is between 6.9 and 11 ounces.
This is generally the approach that should be used to obtain the confidence interval because the previous approach should only be used if it can be assumed that the population standard deviations (which we generally don’t know) are equal.
7.3.2.1 Doing this in R
The assumption that the standard deviations are unequal is specified by default (with the var.equal=FALSE) but it is useful to include this argument for clarity.
# 95% CI
t.test(x=grpN, y=grpS, var.equal=FALSE)$conf.int[1] 6.89385 10.98148
attr(,"conf.level")
[1] 0.95Q7.5 Using the information in Q7.3, calculate the standard error for the difference in mean running times assuming that the standard deviations are not equal and hence calculate the 95% confidence interval. Calculate the degrees of freedom and select the correct multiplier from the following information.
qt(0.975, df=59)[1] 2.000995qt(0.975, df=148)[1] 1.9761227.4 Empirical (bootstrap-based) confidence intervals
In the calculation of confidence intervals so far we have relied on the CLT. In some circumstances, for example if the sample size is very small or the wider (or parent) population is very skewed, we may not be able to safely assume that the distribution of the sample mean is approximately normal. In such cases, the confidence interval may not capture the true parameter with the required level of confidence and so an alternative method for calculating confidence intervals may be more appropriate. An empirical (also called non-parametric or bootstrap) approach is a useful alternative to obtaining a confidence interval.
Assume we want to obtain a CI for a sample mean, then the empirical, bootstrap approach is as follows:
Select \(n\) values at random and with replacement from our original sample of \(n\) values.
- If we have 100 values in the original sample, we randomly select a sample of 100 values.
- Sampling with replacement, means some of the observations in the original data may be selected several times and other observations not selected at all.
Calculate the mean for this generated sample.
Repeat steps 1 and 2 many times (e.g. at least 1000 times).
- For example, if we took 1000 samples each with \(n=100\), this would give us a set of 1000 mean values.
Examine the distribution of these sample estimates and locate the values which define the central 95% of the values in this distribution (whatever it’s shape) (i.e. the 2.5 and 97.5 percentiles).
- These are called ‘percentile’ confidence intervals.
This method has the advantage that,
- it side-steps the assumption that the distribution of sample estimates is normally distributed and simply locates the central 95% of the sample estimates.
- it can be used to obtain confidence intervals for the median or a difference between means, or any other statistic of interest.
However,
- this approach can be computationally intensive,
- and because of the random nature it may not always provide the desired coverage (e.g. the intervals may be too small or too large and may not capture the parameter of interest with the desired confidence).
To illustrate this approach we will use it to find a confidence interval for the mean weights of babies described in Q7.2. To discover more about the bootstrap then see (Davison and Hinckley 1997).
7.4.0.1 Doing this in R
The code below shows the steps involved to generate a bootstrap-based confidence interval for the mean weights of babies born to non-smoking mothers. The numbers relate to the steps outlined above. The weights are stored in an object called grpN.
To repeatedly perform the same commands a ‘for loop’ is used to generate samples and calculate the sample mean; the commands within {} are repeated B times with the index i starting at 1 and increasing by 1 each time the loop is repeated.
# R code to obtain a bootstrap confidence intervals for density
# Number of bootstraps
B <- 1000
# Number of observations
n <- length(grpN)
# Create object to store bootstrap sample means
res1 <- rep(NA, B)
# 3. Bootstrap loops
for (i in 1:B) {
# 1. Generate random sample from data with replacement
bootsamp <- sample(x=grpN, size=n, replace=TRUE)
# 2. Calculate mean of bootstrap sample and store
res1[i] <- mean(bootsamp)
}
# 4. Obtain central 95 percentiles for CI
quantile(res1, probs=c(0.025, 0.975)) 2.5% 97.5%
121.7339 124.2144 Creating a function
If a series of commands are being used repeatedly (as in steps 1 and 2 in the code above), it often makes sense to combine them into a function. This is done in the code below.
samplemean.f <- function(sampdata=data, do.replace=TRUE) {
# Function to generate a sample and calculate the mean
# Arguments:
# sampdata = original sample
# do.replace = indicates whether sampling is with replacement, or not
n <- length(sampdata)
bootsamp <- sample(x=sampdata, size=n, replace=do.replace)
bootmean <- mean(bootsamp)
# Return mean
bootmean
}Defining a function follows certain conventions:
- the first line assigns the function contained in the function to a name (in this case
samplemean.f) - all arguments required for the function are specified at the top, including any default values,
- all function commands are within the parentheses
{} - the last line returns the result of the function.
Having created this function, we can amend the bootstrap code to include it:
# Number of bootstraps
B <- 1000
# Create object to store sample means
res1 <- rep(NA, B)
# 3. Bootstrap loops
for (i in 1:B) {
# 1. and 2. Obtain sample means with function
res1[i] <- samplemean.f(sampdata=grpN, do.replace=TRUE)
}
# 4. Obtain 95 percentiles for CI
quantile(res1, probs=c(0.025, 0.975)) 2.5% 97.5%
121.7559 124.2779 How does this empirical CI compare to that using the conventional method? The CIs obtained from the two methods should be similar; the sample size is fairly large and the heights are approximately normally distributed.
Bootstrapping the easy way!
The commands above have been included to illustrate all the steps in a bootstrap approach. However, in practice we don’t need to write the code to perform such a bootstrap (unless you want to) because R contains a suite of functions which perform these commands; these require two additional libraries to be installed and then loaded into the R workspace with the library function.
The process requires two stages; one to generate the distribution of sample estimates and the second to obtain the confidence interval from the distribution.
The code below generates a CI for mean weight of babies from non-smoking mothers. The oneboot function generates the sample estimates and requires 3 arguments to be specified:
data- the data to be bootstrapped, in this example, the weights are stored in an object calledgrpN,FUN- the name of the function used to calculate the statistic of interest (in this case, we want themeanbut themedianorsd, for example, could also be used), andR- the number of repetitions.
The boot.ci function calculates the CI with the specified level of confidence.
# Bootstrapping CI using built-in functions
# Generate bootstrap sample means
library(simpleboot)
bsmeans <- one.boot(data=grpN, FUN=mean, R=1000)
# Obtain CI
library(boot)
boot.ci(bsmeans, conf=0.95, type="perc") BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates
CALL :
boot.ci(boot.out = bsmeans, conf = 0.95, type = "perc")
Intervals :
Level Percentile
95% (121.8, 124.3 )
Calculations and Intervals on Original ScaleThe CI is similar to those calculated previously but due to the random selection of data, the results from a bootstrap may be slightly different each time the code is executed.
The code below generates a CI for difference in mean weight of babies from non-smoking and smoking mothers using the two.boot function. The arguments are:
sample1andsample2- the two groups of data, in this example, the weights are stored in objects calledgrpNandgrpS,FUN- the name of the function used to calculate the statistic of interest (in this case, we want the difference between the means), andR- the number of repetitions.
# Bootstrapping CI using built-in functions
# Generate bootstrap sample means
library(simpleboot)
bsdiffs <- two.boot(sample1=grpN, sample2=grpS, FUN=mean, R=1000)
# Obtain CI
library(boot)
boot.ci(bsdiffs, conf=0.95, type="perc") BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates
CALL :
boot.ci(boot.out = bsdiffs, conf = 0.95, type = "perc")
Intervals :
Level Percentile
95% ( 6.845, 10.975 )
Calculations and Intervals on Original Scale7.5 Confidence intervals for other sample statistics
The methods described in this chapter can be adapted to find confidence intervals for other sample statistics, for example the median and variance. As previously mentioned, bootstrap confidence intervals can easily be obtained for these sample statistics in R by changing the FUN argument in the one.boot or two.boot functions.
Parametric confidence intervals can also be obtained in a similar manner to that of the sample mean. Rather than using the \(t\) distribution other statistical distributions are used; for example, for a CI for the variance a \(\chi^2\) distribution is used - this distribution is described in Chapter 12. A brief description of a CI for the median is given below. In a later chapter we look at confidence intervals for sample proportions.
7.5.0.1 Confidence interval for the median
For the median, the confidence interval is obtained slightly differently and because we are not making any assumptions about the distribution (e.g. that it is symmetric), the CI is approximate.
Similar to the median, the CI is based on ranked values. The ranked value for the lower 95% CI (for a sample of size \(n\)) is given by
\[\frac{n}{2} - \frac{1.96 \sqrt{n}}{2}\] and the ranked value for the upper 95% CI is given by
\[1 + \frac{n}{2} + \frac{1.96 \sqrt{n}}{2}\]
The CI is then obtained by finding the observed values associated with these ranked values.
Example The median weight of babies is 120 ounces. The sample size is 1236 and so the median was the average of the 618th and 619th ranked values. The ranked value for the lower 95% CI is found from
\[\frac{1236}{2} - \frac{1.96 \sqrt{1236}}{2} = 618 - 34.45 = 583.55\]
The ranked value for the upper 95% CI is found from
\[1 + \frac{1236}{2} + \frac{1.96 \sqrt{1236}}{2} = 1 + 618 + 34.45 = 653.45\]
There are no ranked values 583.55 and 653.45 and so these values simply get rounded to the nearest integer, hence, the 584th and 653rd ranked observations provide the confidence interval, which in this case is 119 to 121 ounces.
Note that the confidence interval may not be symmetrical about the median because it is based on ranked values.
7.5.0.2 Doing this in R
To obtain a CI for the median, we again make use of a function, wilcox.test, that we will come across again later in the course but for now we use it to harvest the CI.
# Calculate median
median(baby$bwt)[1] 120# 95% CI for median
wilcox.test(x=baby$bwt, conf.int=TRUE)$conf.int[1] 119 121
attr(,"conf.level")
[1] 0.95An alternative method (there are others) requires the package DescTools to be installed and loaded and then the function medianCI can be used:
# Load library(already installed)
library(DescTools)
# 95% CI for median
MedianCI(baby$bwt)median lwr.ci upr.ci
120 119 121
attr(,"conf.level")
[1] 0.95035557.6 Summary
This chapter has illustrated that sample estimates, such as the sample mean, follow statistical distributions and we know something about the location and spread of these sampling distributions based on the information in the sample (i.e. sample size, mean and standard deviation). This information can be used to obtain a plausible range of values for the true, but unknown, population mean: a confidence interval.
7.6.1 Learning outcomes
In this chapter you have seen:
- that the sampling distribution of a sample estimate is normally distributed which has led to the Central Limit Theorem,
- the calculation of confidence intervals, for both a sample mean and the difference between two sample means, relying on the CLT, and
- the calculation of bootstrap-based confidence intervals,
- and that confidence intervals can be obtained for other sample statistics.
7.7 Answers
Q7.1 a. The standard error is 4.2426 cm from
\[se(\hat \mu) = \frac{s}{\sqrt{n}} = \frac{30}{\sqrt{50}} = 4.2426\]
Q7.1 b. The correct multiplier for a 90% confidence interval when using the sample standard deviation is qt(p=0.95, df=49) = 1.6765
Q7.1 c. The 90% confidence interval is 757.9 to 772.1 cm, calculated from
\[765 \pm 1.6766 \times 4.2426\]
Q7.1 d. We can be 90% confident that the mean diameter at breast height is between 757.9 to 772.1 cm.
Q7.2 The 95% confidence interval is given by
\[\hat \mu \pm 1.96 \times \frac{s}{\sqrt{n}}\]
and substituting in the numbers gives
\[123.05 \pm 1.96 \times \frac{17.4}{\sqrt{742}}\] \[123.05 \pm 1.96 \times 0.6388\]
\[123.05 \pm 1.252 \] \[121.8 \quad ; \quad 124.3\]
The sample mean is 123.05 ounces with a 95% confidence interval (121.8, 124.3).
Q7.3 The mean running time for each brand are
\[\hat \mu_A = \frac{4451}{90} = 49.46 \quad ; \quad \hat \mu_A = \frac{2763}{60} = 46.05 \] An estimate of the difference in mean running time is 3.41 minutes:
\[ \hat \mu_A - \hat \mu_B = 49.46 - 46.05 = 3.41\]
Q7.4 Assuming that the standard deviations are equal, the standard error is given by
\[se(\hat \mu_A - \hat \mu_B) = s_p \sqrt{\frac{1}{90} + \frac{1}{60}}\] where
\[s_p = \sqrt{\frac{89 \times 6.32^2 + 59 \times 3.31^2}{90 + 60 -2}} = \sqrt{\frac{4205.195}{148}} = 5.33 \] \[se(\hat \mu_A - \hat \mu_B) = 5.33 \times 0.1667 = 0.888\]
The 95% confidence interval for the difference is mean running time is 1.65 to 5.17 minutes.
\[ 3.41 \pm 1.976 \times 0.888\]
Q7.5 Assuming that the standard deviations are not equal the standard error is given by
\[se(\hat \mu_A - \hat \mu_B) = \sqrt{\frac{6.32^2}{90} + \frac{3.31^2}{60}} = 0.792\] Using the simple approach to obtaining the multiplier, the required degrees of freedom are 59 (i.e. the minimum of 59 and 89), thus the multiplier is 2.001. Substituting in these values, the 95% confidence interval for the difference in mean running time is now between 1.8 and 5 minutes:
\[3.41 \pm 2.001 \times 0.792\] \[ 1.825 \quad ; \quad 4.995\]