Chapter 2 Data collection and Sampling
2.1 Introduction
Statistics deals with techniques for collecting and analysing data in order to draw conclusions or make some inference. This chapter outlines processes which are used to obtain data in order to draw sound conclusions. The basic techniques incorporate some form of random sampling. This chapter describes the need for sampling, basic sampling strategies, common problems that can afflict the sampling process, and the terminology required.
By the end of the this unit, you should be able to:
understand the basic principles of sampling
appreciate the sorts of biases that may occur
distinguish between accuracy and precision
understand the difference between experiments and observational studies.
2.1.1 Terminology
We need a common language to talk concisely about statistics and here introduce terms related to sampling that will be used throughout the course:
Sampling unit : an individual object, animal, or person, on which measurements can be made. Essentially this is a discrete entity which is the basis of statistical inference.
Target population: the overall collection of potential sampling units about which we want to make some inference.
Census: when the entire target population is sampled/measured.
Sampling protocol or design: the procedure, or strategy, for selecting sampling units from the target population.
Sample: a subset of the target population for which measurements on sampling units are made.
Variable: a characteristic defined for each sampling unit (e.g. age, weight, blood group) and are typically denoted by lower case Roman letters (e.g. \(x\), \(y\) represent vectors containing measurements for each sampling unit).
Parameter: a numerical summary for the target population (e.g. the mean height of adults in the UK) and are typically denoted by Greek letters (e.g. \(\mu\), \(\sigma\)) or a numerical characteristic of a statistical model.
Estimate/Statistic: a numerical summary of a variable for the sample (e.g. the proportion of a sample of UK citizens that favour a particular political party). Different notation conventions apply to represent estimates from samples, but generally lower case Roman letters are used (e.g. \(\bar x\) represents the mean of sample data denoted by \(x\)). Note, these statistics are often estimates of a population parameter (e.g. \(\bar x\) estimates \(\mu\)).
2.2 What is sampling and why do it?
Suppose a landowner has 200 acres of forest where the trees ready for harvest and plans to sell the timber; how could we determine the volume of wood from the forest to get an idea of monetary value? A tree could be a sampling unit and one approach would be to visit every tree, measure its total height, diameter at various heights and calculate the volume. We may also want to “grade” the tree in terms of percentage of good wood, lack of defects, decay, etc. In essence, we would be conducting a census of the trees. However, visiting and measuring every tree could be prohibitively expensive, taking far too much time and money.
Therefore, we don’t measure all the trees but instead take a sample of plots of land (i.e., a subset of the forest), estimate the volume and grade of trees for each subset. From this the average volume on a plot can be obtained and multiplying this by the total number of plots in the forest will result in an estimate of the total volume of wood in the forest.
In this example, the trees are not necessarily damaged by measuring. In some cases, however, taking a measurement can involve damaging or destroying the unit involved. For example, quality control testing of cans of fizzy drink may involve opening the cans to measure the contents. Taking a census (or indeed sampling a large proportion of the target population) would be clearly counter-productive.
In many cases, it may not be necessary to know the true (i.e. population) parameter and an estimate will be sufficient. For example, we may not need to know the true volume of wood in the forest and an estimate will be good enough to get an idea of the monetary value of the forest. Therefore, sampling is used rather than take a census. This may be because because we can’t measure the entire population: it would be too expensive, take too much time and effort, is impractical or impossible.
2.2.1 Precision, accuracy and bias
In sampling, we take a sample from a target population and generate a statistic of interest. Suppose we are interested in establishing the proportion of undergraduate students in the University of St Andrews who have a driving licence. We might select a sample of students, ask them whether they have a driving licence and calculate the sample proportion. Image repeating this process with many samples of students. It is likely that the sample proportion will be different for each sample. Ideally, we would like our statistic to be accurate, precise and unbiased (top right in Figure 2.1), where
accuracy implies that each sample statistic is similar to the population parameter
precision implies that the value of the sample statistic is similar for all samples, and
bias implies that the sample statistic tends to differ from the population parameter in some consistent way (i.e. there is a systematic error).
In general, a sample statistic will be some combination of the population parameter being estimated plus any bias and some random variability.
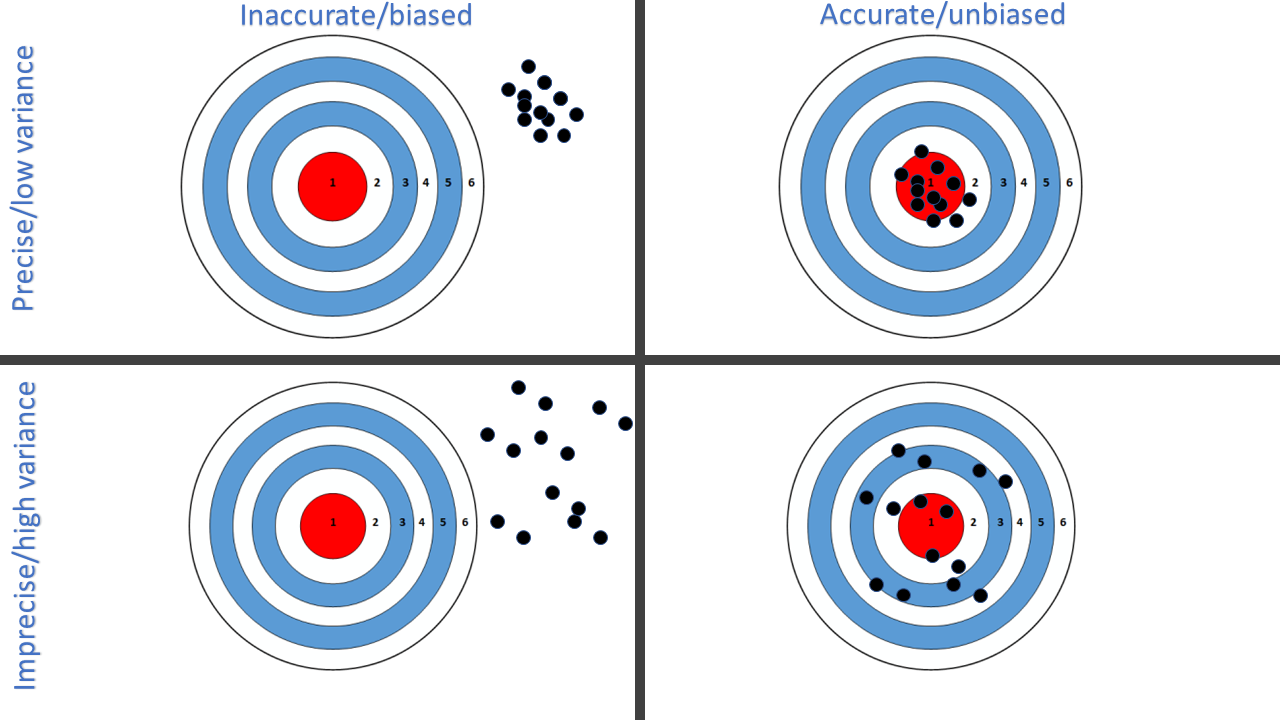
Figure 2.1: The centre of the target indicates the true value of the parameter and the dots are sample statistics.
Q2.1 A headline on the BBC website stated that “Vapers rise ‘to more than three million’ in Britain” (BBC, 14/09/2018). The article goes onto state that the numbers of e-cigarette users has risen from from 2.9m to 3.2m between 2017 and 2018 - a rise of 10%. It is likely that a sampling survey has been undertaken to obtain these numbers.
a. What is the target population?
b. What is the sampling unit?
c. What is the variable being measured?
d. What is the population parameter?
e. What is the sample estimate?
2.3 Three types of data collection
There are three general procedures for collecting data and each are covered in this chapter:
sample surveys (and polls)
designed experiments
observational studies.
Statisticians make a distinction between experiments and observation studies (also known as quasi-experiments).1
It is important to emphasise that how data are collected affects the ability to learn about the world. Flawed data collection procedures can make it impossible, or nearly so, to arrive at quality decisions or to make accurate statements. In many cases, no amount of sophisticated data analysis procedures will remedy “bad data.” Notably, whatever method is used for the collection/generation of data, sampling is likely to underpin the collection process. From the outset there is inherent uncertainty surrounding our ability to produce answers for a population from a sample, hence, robust sampling strategies need to be used when selecting a sample.
2.3.1 Common, but unwise, data collection strategies
For sample estimates to be applicable to the target population from which the sample was taken, the sample needs to be representative. Two approaches to sampling which generally lead to unrepresentative (i.e. biased) samples are anecdotal evidence and self-selected samples.
Anecdotal evidence can be based on haphazardly selected individual cases, which often come to our attention because they are striking in some way. These cases need not be representative of any larger group of cases.
Self-selected, or voluntary response, samples are commonplace; magazines and newspapers often include questionnaires that readers can complete and send back. Internet polls are much the same, as are opt-in surveys: individuals choose whether or not they want to respond and hence be included in the sample.
Principally, we want any sample statistic to have:
high precision/low uncertainty,
high accuracy, and hence low bias,
as per top right panel in Figure 2.1. There can be many sources of inaccuracy and/or a lack of precision, but fortunately some of them can be controlled. Sampling is a just such a controllable source and three frequently used strategies are described below.
Q2.2 Considering phone-in programmes on the radio, are the opinions expressed representative of the UK population, or even of all the people who listen to the radio show? What type of person is likely to call?
2.4 Simple sampling approaches
Having decided to take a sample from our target population, the next question is how to choose the sample. All good sample schemes have two features:
planned randomness, and
the chance, or probability, that any given sampling unit being selected can be calculated.
These features ensure that sample is representative of the population; i.e., one has controlled for selection bias, the bias that results when part of the target population is systematically excluded from the samples.
Sampling is a large topic of study in itself; here we consider three basic strategies:
Simple random samples
Systematic random samples
Stratified random samples
2.4.1 Simple random sample
A simple random sample (SRS) is a subset of the target population in which each sampling unit has an equal chance of being selected. The chance, or probability, of a sampling unit being selected can be calculated easily. Say the target population is of size \(N\) and the sample size is \(n\), then the probability of an individual sampling unit being selected is \(n/N\).
Example We want to select 10 students from a group of 150 using simple random sampling. The probability of an individual student being selected is \(\frac{10}{150}\).
How do we ensure that each sampling unit has an equal chance of being selected? One way would be to assign a number to each individual, write each number on a slip of paper, put the slip of papers in a hat, mix thoroughly and draw 10 slips out - the numbers on the slips of paper determine who is selected. Alternatively, a computer could be used to generate 10 numbers from a list of numbers 1 to 150.
2.4.1.1 Doing this in R
# Generate a simple random sample of size 10 from a population of 150 units
# Initialise necessary objects
N <- 150 # Size of target population
n <- 10 # Sample size
# SRS
sample(x=1:N, size=n, replace=FALSE) [1] 33 9 37 119 115 114 139 85 50 131# The sample doesn't have to be numbers
IDs <- c("subject1", "subject2", "subject3", "subject4", "subject5")
sample(x=IDs, size=2, replace=FALSE)[1] "subject4" "subject1"It is worth spending a minute thinking about computer-generated random numbers. Computers are not random, however, they can be ‘effectively’ random with pseudo-Random Number Generators (RNGs). There are many types of RNGs, but all are effectively unpredictable without knowing a starting point. In the examples below, we generate a sample of numbers with and without specifying the starting point.
First, we don’t specify the starting point and so each time we generate a sample of numbers, the samples are different.
# Example when the result is unpredictable
# Generate 4 decimal numbers from 0 to 1 (a uniform (0,1) distribution)
runif(n=4, min=0, max=1)[1] 0.3839566 0.1328483 0.6887229 0.1039757# Repeat
runif(n=4, min=0, max=1)[1] 0.2096631 0.5713851 0.4916080 0.4418365But - with a seed, a starting point for the RNG, the generated numbers are predictable/reproducible.
# Set the seed for the RNG
set.seed(2343)
runif(n=4, min=0, max=1)[1] 0.20467634 0.09047926 0.61101041 0.17877428# Repeat
set.seed(2343)
runif(n=4, min=0, max=1)[1] 0.20467634 0.09047926 0.61101041 0.17877428Setting the seed is useful for confirming calculations which have a stochastic, or random, component.
2.4.2 Systematic samples
Suppose there are \(N=1000\) individuals in the target population and we want to take a sample of size \(n=200\). A systematic sample can be selected as follows:
Calculate the fixed periodic interval, \(k = N/n\). In our example, this is \(k = 1000/200 = 5\).
Randomly pick a starting number between 1 and \(k\), call it \(q\), say \(q=3\)
Sample the \(q\)th individual, then the (\(q+k\))th, then (\(q+2k\))th and so on. Thus, starting at \(q=3\), the sample will be generated by 3, (3+5), (3+2x5), and so on; the sample will consist of sampling units 3, 8, 13, …, 993, 998.
Systematic samples have some advantages over SRS:
it is often easier to draw since only one number is randomly selected (i.e. \(q\)).
it will distribute the sample more evenly through the population.
it will do better than a SRS if there is a trend in the values.
Example We want to take a sample of customers visiting a bank. From a practical point of view, it is much easier to pick every 10th person, say, arriving in the bank than refer to a SRS of bank customers. In addition, SRS could, by chance, select a lot of customers in the morning which could be a particular subset of the customers if there is a pattern in the type of customers that arrive through the day. A systematic sample would spread the selected customers throughout the day.
One thing to be aware of is, if the population contains some variation which is periodic in nature and if the fixed periodic interval (\(k\)) equals the periodic variation, the sample may be biased. Consider loaves of bread on a production line; each loaf is cut into 20 slices. A slice is taken from each loaf. Using a systematic sample with a fixed interval of \(k=20\), the sample will consist of either all crusts or no crusts, depending on the starting value.
2.4.2.1 Doing this in R
The code below selects a systematic sample.
# Draw a systematic random sample of size 20 from a population of 100 units
# Initialise values
N <- 100 # Size of target population
n <- 20 # Sample size
# Calculate fixed periodic interval k
k <- N/n
k[1] 5# Randomly select starting point q
q <- sample(1:k, size=1)
q[1] 3# Generate regular sequence
seq(from=q, to=N, by=k) [1] 3 8 13 18 23 28 33 38 43 48 53 58 63 68 73 78 83 88 93 982.4.3 Stratified random samples
In a stratified random sample, the population is divided into different groups or “strata,” then simple random samples are selected from each stratum. For example, we might divide the population of the university into four strata (e.g. undergraduate students, postgraduate students, academic and research staff, and support staff) and take a SRS from each strata. Why do this?
Sometimes it is more convenient to organise sampling in this way and choose a SRS within a homogeneous group.
The stratification ensures that all strata will be represented in the overall sample, which may not be the case for a SRS.
It may be useful to examine the separate statistics from each strata.
It can result in greater precision when estimating a parameter than for a SRS with the same sample size because sampling units within a stratum may be more similar (hence reducing variability).
The size of the sample in each stratum can be proportional to the total number of sampling units in each stratum so that each stratum is represented equally.
The proportion of sampling units in stratum \(i\), \(p_i\), can be found from
\[p_i = \frac{N_i}{N} \] where \(N_i\) is the total number of sampling units in stratum \(i\). For a total sample of size \(n\), then the number selected from group \(i\) can be calculated from \[n_i = n \times p_i\]
This strategy is frequently used in environmental studies, for example, in fisheries stock assessment where different areas (strata) are sampled with different intensity.
Q2.3 In 2019, the population of the University of St Andrews was made up of members classed in one of four groups (size of the group is given in parentheses):
undergraduate students (7,221),
postgraduate students (1,763),
academic and research staff (1,426), and
support staff (1,174).
a. For a simple random sample of size 500, what is the probability of an individual member of the University being selected?
b. If we take a systematic sample of size 500, what is the fixed period interval, \(k\)?
c. Assume that all members of staff are assigned a number. Given a starting number of \(q = 12\), what are the first five numbers of a systematic sample that would be selected using the value of \(k\) calculated in part 2a?
d. We now want to take a stratified random sample, using the groups as the strata, and sample in proportion to the strata sizes. What will be the sample size for each group if the total sample size is 500?
2.5 Sampling biases
Sampling error is incurred when the characteristics of interest in a population are estimated from a sample - it is the difference between the sample statistics and the true, but unknown, parameter of the population - and is unavoidable. There will also be random variation between samples - sampling error is also used more broadly to refer to this sample-to-sample variation. Therefore, it is important that our samples are representative of the population as a whole. In essence, we want any differences between our samples and the population to be due to random variation only and not due to other sources of error.
Selecting a sample in such a way that it is unrepresentative of the target population has been mentioned and will cause bias, however, even if a random sample is selected in some way, then serious biases can still occur.
2.5.1 Non-sampling error
Even though a random sample has been selected, sources of error, or bias, can occur when collecting data. A few common sources of error when surveying people in particular are listed below.
Non-response bias
When surveying people, a certain percentage of the sample will not provide information even though they have been selected to take part. The reasons for non-response will be many and may include not being at home, too busy, or having a dislike for pollsters. If the values of the variable(s) being measured differs between non-responders and responders, then the resulting statistic can be severely biased.
Survey format
The format of a survey (e.g. postal questionnaire, by telephone, in person) may affect the results. For example, respondents may not feel comfortable giving personal information to an interviewer (e.g. “How old are you?”) but more willing to provide the information in a postal questionnaire.
Question effects
Questions can be slanted in a particular way, or lead the respondent on purpose; for a well-designed survey this should be guarded against. The choice of words is also important as the following example illustrates.
Example (from (Moore and McCabe 2003)) When asked ‘How do the Scots feel about the movement to become independent from England?’ 51% of the sample voted for “independence for Scotland,” but only 34% supported “an independent Scotland separate from the United Kingdom.” It seems that the wording of the question had an effect; maybe “independence” is a nice, hopeful word while “separate” is a negative word.
Poor quality data can also arise depending upon length of survey; the respondent may get tired or bored if there are too many questions, or question response categories, to consider. The questions should also be in some logical order and not jump between topics which may confuse the respondent.
Response bias
The behaviour of the respondent or of the interviewer can influence responses in several ways.
An interviewer can intimidate or alienate the respondent, albeit unintentionally (e.g., different race or social class) leading the respondent to answer untruthfully.
A respondent may not answer truthfully because a question may have:
a social stigma (or legal implications) related to it (e.g. “Have you ever been arrested?”)
a social prestige slant (e.g. “How much money do you earn?”).
Respondents may
answer in a way that is socially acceptable (e.g. to the question “How many units of alcohol do you drink per week?”)
suffer from recall bias so that they cannot remember exactly when something happened or what happened (e.g. “How many hours of television did you watch last Thursday?”)
misunderstand the question (e.g. giving weight in kilograms instead of pounds).
Careful and thoughtful questionnaire design is important\footnote{Further reading can be found here. Any questionnaire should be tested to eliminate any inconsistencies or confusion before it is used for real.
Q2.4 In 1936, a magazine in the USA called the sent out 10 million questionnaires to people drawn from car registration lists and telephone directories asking who they would vote for in the upcoming election; 2.3 million questionnaires were returned. From the results, the magazine predicted a landslide victory for Republican candidate Alf Landon. In fact, the Democrat candidate, Franklin Roosevelt, won the election. With such a large number of questionnaires returned, what do you think went wrong?
Q2.5 A psychologist was interested in understanding the motivation of serial killers and in estimating the mean number of victims per serial killer. The psychologist discovered there were 261 serial killers incarcerated worldwide.
a. The psychologist initially planned to interview all imprisoned serial killers about various aspects of their personality. Describe the approach being used.
b. This initial approach proved to be too costly, therefore, the psychologist randomly choose 80 killers to contact and ask if they were prepared to be interviewed. Thirty-nine agreed to be interviewed. Comment on the representativeness of the sample to the whole population of worldwide serial killers and what type of bias this may result in, if any.
c. In choosing the initial 80 prisoners, the psychologist selected them randomly in proportion to the overall number of imprisoned serial killers in each country e.g. if 50% of the world’s convicted serial killers were in prisons in the USA, then 40 serial killers in the USA were selected at random. What sort of sampling design is this?
2.6 Experiments
The (Anonymous 1980) gives the following definition (one of several) for an experiment: An action or operation undertaken in order to discover something unknown, to test a hypothesis, or establish or illustrate some known truth.
In an experiment, we often try to discover whether a “treatment” or “condition” has an effect on sampling units, or experimental units, and what the nature and magnitude of that effect is. Typically there is a manipulation or intervention. Note that if the experimental units are animals, they are known as “subjects” and if the experimental units are humans they are increasingly referred to as “participants.” Experiments do not have to be done in the laboratory, they can be undertaken anywhere, for example, experiments might be used to answer the following questions:
- Does a certain drug improve the prospects for heart transplant patients?
- Does heating a wire increase its electrical resistance?
- How effective is an insecticide?
To investigate these questions, we give different treatments to different experimental (sampling) units and measure a response. In the examples, above, these might be:
| Example | Experimental unit | Treatment |
|---|---|---|
| 1 | patient | drug |
| 2 | wire | heat |
| 3 | mosquito | insecticide |
There is often some natural variability in the results of any experiment. Using statistics, we aim to disentangle this natural variation from any variation that is introduced by our treatment method.
2.6.1 Randomised experiments
In a randomised experiment, treatments are randomly allocated to experimental units by the researcher.
Example A new drug for heart-transplant patients is to be tested against a standard drug. Patients in the study are randomly allocated to either the new or standard drug group. Each patient in the heart-transplant study has an equal chance of being selected for the group that will be given the new drug.
A difference in the response between the two groups can be attributed to the treatment because the patients were randomly allocated to treatments.
Example A new insecticide is developed for the control of mosquitoes for use in countries where malaria is a significant problem. How effective is it, and will it be cheaper or more expensive to use than existing chemical treatments?
The insecticide is designed for use with adult mosquitoes and a scientist might set up an experiment like this:
Create 4 separate enclosures
Place a sample of the same number of adult mosquitoes in each enclosure.
- These individuals are the experimental units in this experiment.
Choose 4 different concentrations of insecticide, one for each enclosure.
- Apply the treatment each day by spraying enclosure with insecticide.
- The concentration of insecticide is a factor known as the explanatory variable.
One treatment should be a control in which no insecticide is applied, but a water spray is applied (in case mosquitoes are actually killed when sprayed).
Determine how many mosquitoes in each enclosure survive, and how many die (mortality, in this case, is the response variable/variable of interest).
Repeat (replicate the whole experiment) 10 times.
- We can then see how much natural variation occurs in the results of the experiment
- this enables us to determine whether the treatment has a real effect on the outcome or if any differences are down to natural variability alone.
Randomly assign experimental units (mosquitoes) to the 4 treatments and 10 replicates. This should get around possible biases
- e.g. if “fitter” individuals are selected for one treatment.
- Differences in responses should then only be due to the effect of the treatments.
2.6.2 Components of an experimental design
Randomization may be carried out by assigning numbers to individuals, then picking numbers at random. Randomization is done to ensure that treatment groups are, on average, similar.
- Randomization is designed to avoid bias.
Replication is carried out in order to:
assess the amount of natural variation in the results. This way, it is possible to determine whether a treatment has a significant effect.
increase precision. The more replicates, the more precise the result (but the greater the cost in time and money!)
As a rule of thumb, the number of replicates should be at least twice the number of treatments with an absolute minimum of 6 per treatment.
Sometimes, the experimental units (or subjects) are partitioned into stratum, or blocked. For example, in the mosquito experiment, individuals could be assigned to “male” and “female” groups (strata) before being randomly allocated to a particular treatment. This may reduce the amount of natural variability in the results of an experiment, so that the results are more precise.
In studies involving human subjects, for example in drug trials, a placebo may be given to a control group.
A placebo is a ‘treatment’ (e.g. drug or intervention) with no known active effects e.g. sugar pills.
It is given so that the patient does not know what treatment they are receiving because there may be a psychological effect when a doctor offers a patient a treatment.
It may also be necessary to use double blinding so that the doctor does not know what treatment they are offering and the patient does not know what treatment they are receiving. This avoids subtle differences in the behaviour of doctors according to the treatment they are prescribing.
If a randomised experiment shows a significant effect, it is possible to argue for causation i.e. that the treatment caused the effect.
Example A famous and large-scale designed experiment that is still relevant today is Salk’s polio vaccine study.
Polio (poliomyelitis) is a serious viral infection that used to be common worldwide. It caused muscle weakness from which a small percentage of people did not recover and even died. The number of cases in the US during the mid 20th century are shown in Figure 2.2.
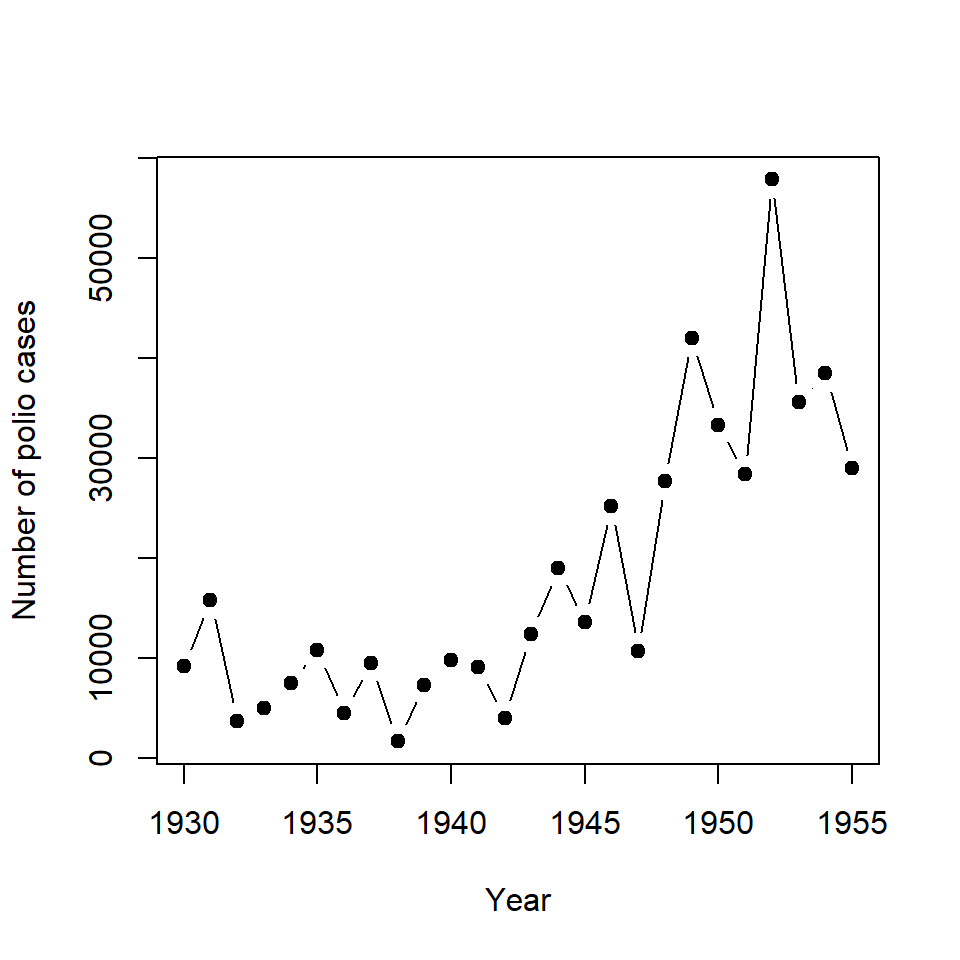
Figure 2.2: The number of polio cases from 1930 to 1955.
- In general, the incidence of polio was increasing over this time period.
- However, the incidence of disease also fluctuates from year to year, with high and low incident years sometimes alternating.
Jonas Salk created a vaccine and a large-scale trial of this vaccine was conducted in the US in 1954 to determine how effective it was in protecting children from paralysis or death due to polio. Snedecor and Cochran (1980) describe the study in detail; a summary is provided here. School children were divided into two groups; one group received the vaccine (the treatment group) and the other group received no vaccine (control group). The comparison of the numbers of paralytic cases in each group were used to judge the effectiveness of the vaccine. Since severe symptoms are rare, large numbers of children were required and more than 200,000 children were recruited to each group. Within each participating school, children were randomised such that there were about equal numbers of children in each group. This stratified approach ensured that schools in high risk and low risk regions had about equal numbers of children in each group. A simple randomisation of children to the groups would mean that overall the numbers in the two groups were equal but would not take account of high and low risk regions.
The children in the vaccine group received three injections of the vaccine and the children in the comparison, or control, group received three injections of a saline solution. They were given at the same time and in the same manner. A crucial aspect of the study was that neither parents, children, medics administering the vaccine or the doctors diagnosing illness knew which treatment group the children were in - this was a double-blind trial.
The following table shows the numbers of children in each of the groups and the number of polio cases ((Snedecor and Cochran 1980), pg. 13):
| Group | Number of children | Polio cases per 100,000 |
|---|---|---|
| Vaccinated | 200,745 | 16 |
| Control | 201,229 | 57 |
The trials provided good evidence for the effectiveness of the vaccine. Regular use of polio vaccine since the Salk trial has reduced the incidence of the disease dramatically.
To summarise, in an experiment we often try to determine whether a ‘treatment’ (or intervention of some kind) has a significant effect.
A control group is a group of units that are not exposed to the treatment. This group is generally necessary for comparison with the treatment group to assess the effectiveness of the treatment.
In a randomised experiment, subjects/experimental units are assigned to the treatment or control group at random.
In blocked experiments, the experimental units may first be divided into strata or groups (e.g. on the basis of age).
Experiments should be replicated.
In drug trials, patients in the control group may be given a placebo (an inactive pill or medicine) so that they do not know whether they are in the control or treatment group
If the doctor also does not know which group the patient is in, this is a double-blind trial
If a randomised experiment produces a significant effect, then we can argue for a causal link between treatment and effect.
2.6.3 Controls
Controls are benchmarks required for a comparison, they are frequently used but not necessarily essential. For example, one might be interested in knowing whether having a cup of coffee elevates heart rate. Here a control is essential, otherwise how would one know if an elevation in heart rate was due to the coffee or because the heartbeat was being measured.
Sometimes a control is not necessary, for example if the question was “Do different sorts of coffee have different effects on heart rate?” The natural experiment would be to compare different varieties of coffee, no control is required because, here, we have a contrast.
Q2.6 A doctor is investigating the potential effect of a new drug in combating an as yet incurable disease. Is a control required?
Q2.7 A pharmaceutical company is testing whether a new experimental drug is better than the existing treatments on the market. Is a control required?
2.7 Observational Studies
Observational studies refer to data collected from ‘nature’ without any kind of manipulation and so conditions are NOT under the control of the researcher. This terminology is commonly used across most of science, however alternative terminology is sometimes used; astronomers often refer to theory-based observation of stars, galaxies, gas clouds as “experiments” although in no sense are they manipulating the cosmos!
Example Let us return to the mosquito example. Imagine that villagers have already been using the new insecticide in the field. They have used the chemical at various concentrations. A scientist surveys the area and determines the population density of mosquitoes in different locations. This scientist also collects information from the local people as to what concentration of insecticide they have been using.
This looks quite similar to the previous study. However, the results are more difficult to interpret because:
we do not know if there are naturally-occurring differences in mosquito population density in the different areas due to “other factors.” For example, there may be other animals that eat mosquitoes in one area and so the density is reduced (a confounding variable).
we do not know that the mosquitoes themselves are “all the same,” e.g mosquitoes in one area may be genetically different to those in another area (another confounding variable).
It is more difficult to argue for causation based on an observational study because of potential confounding variables. It is important to remember this when reporting on the outcome of a statistical investigation. However, in practice, observational studies often have to be used as evidence for an effect because:
It may be difficult, in practice, to carry out a randomized experiment, e.g. the effects of fishing on a large ecosystem such as the North Sea cannot be explored by conducting experiments on a series of “replicate” oceans.
It may be unethical to carry out a randomized experiment:
- e.g imagine that we want to know about the implications of smoking for human health. We are interested in knowing what effect of mothers smoking during pregnancy has on the average birth-weight of babies. It would not be ethical to ask a randomly-chosen group of mothers to take up smoking, because this might adversely affect their unborn babies or their own health.
Therefore, we have to examine other kinds of evidence:
- randomised experiments carried out on animals
- observational studies, e.g. looking at birth weights of babies born to mothers who have chosen not to smoke and weights of babies born to mothers who have chosen not to give up smoking in pregnancy.
Remember that an observational study is not a randomized experiment, we may not be able to make a strong argument for causation based on the results. For example, if it is found that babies where the mothers smoked during pregnancy have generally lower birth weight, this could be due to confounding variables, such as diet.
2.7.1 Types of observational study
There are a variety of types of observational study. Some of which are given specific definitions:
Cohort study: A cohort is any group of people who are linked in some way. For instance, a birth cohort includes all people born within a given time frame. Researchers compare what happens to members of the cohort that have been exposed to a particular variable to what happens to the other members who have not been exposed.
Case control study: Researchers identify people with an existing health problem (‘cases’) and a similar group without the problem (‘controls’) and then compare the two groups with respect to an exposure or exposures.
These studies can be prospective or retrospective:
Prospective: none of the subjects have the disease (or other outcome of interest) when the study commences; the subjects are followed over a period of time to determine whether the disease develops.
Retrospective: the researcher looks at historical data to examine previous exposure to suspected factors in relation to an outcome determined at the start of the study.
Example UK Millennium cohort study
Known as the ‘Child of the New Century’ project, the lives of nearly 19,000 children born in the UK during 2000 and 2001 were followed. Data were collected when they were 9 months, 3, 5, 7, 11, 14 and 17 years. A large number of studies have been conducted of the data collected looking at, for example, health, behavioural problems, career aspirations. Details can be found here
Example A retrospective, case control observational study on smokers
To determine the death rate of men with different smoking habits, large studies were undertaken between 1951 and 1959 (1980). A questionnaire was sent to the selected group of men asking about current and past smoking habits and other information, such as age. The study compared different groups whose death rates could be compared (e.g. different types of smokers - nonsmokers, cigarettes, cigars, pipes, mixed).
If death rates were found to be different between the groups it would still be difficult to conclude this was due to the smoking habits. The subjects assigned themselves to groups by their smoking habits and the groups may differ in other ways apart from their smoking habits (e.g. age, income, lifestyle).
To control for other factors, the researchers must try to control for these other factors and divide the subjects into groups such that these other factors are similar. Then, for example, compare the death-rates of smokers and non-smokers who are in the same age category.
Example A retrospective, case control study on sudden infant death syndrome (SIDS)
A large study on SIDS cases in Scotland were investigated from 1992 to 1995. When a case of SIDS occurred, the parents were interviewed to find out about methods of infant care and socioeconomic factors. Two controls were chosen for each case by identifying babies born in the same maternity unit and just before/after the SIDS baby, thus controlling for time of year and age and maternity unit. More details here
To summarise, there are two main types of observational study, cohort and case control studies.
A prospective study is one in which samples are chosen, and variables measured, and the subjects (or units) are subsequently observed over time in order to observe the outcomes. The relationship between the initial measured variable on the outcome can be studied.
In a retrospective case-control study, cases in which a certain outcome has occurred are compared with controls in which that outcome has not occurred. Differences between the case and control groups may indicate factors that are correlated with certain outcomes.
A confounding variable is some factor not accounted for, which introduces a difference in outcomes between treatment groups that is NOT due to the effects of the treatment.
It is generally not possible to infer causation from an observational study: it is difficult to exclude the possible effects of confounding variables.
2.8 Observational studies vs experiments
Observation studies have advantages in that they:
- can often be cheaper, the results are collected from observation rather than requiring active intervention.
- effects can be investigated that would be unethical to manipulate e.g. the action of living near nuclear waste depositories on the risk of cancer - people cannot be foreced to live near nuclear power stations.
Experiments have advantages in that they:
- allow the investigation of variables that might not occur naturally
- causation can be easier to infer if there has been a direct manipulation.
Q2.8 An evil industrialist has deliberately created an oil spill to prevent an area being recognised as a conservation zone. You as a statistical ecologist are conducting a survey of species diversity to compare to an earlier survey done prior to the oil spill? Is this an experiment or observational study?
Q2.9 The evil industrialist is also a statistical ecologist and he conducts and analyses a survey of the polluted area. Is this an experiment or observational study?
2.9 Summary
Any well-designed sampling survey needs to have some random component included when selecting the sampling units in order to avoid bias. Several strategies can be implemented to select the sample depending on the aim of the study. However, even with a randomly selected sample, non-sampling biases can occur, particularly when studying people. Therefore, careful thought is required to decide what data to collect and how to collect it. In randomised designed experiments one can argue that some treatment, or intervention, has caused the observed effect. However in some situations, experiments are not appropriate and so observational studies are used.
Further reading on the subject can be found in (De Veaux, Velleman, and Bock 2006) or (Wild and Seber 1999).
2.9.1 Learning objectives
This unit has covered:
the basic forms of data collection
the basic principles of sampling and illustrated different sampling strategies,
illustrated the difference between accuracy and precision,
highlighted the sorts of biases that may occur and
described the differences between designed experiments and observational studies.
2.10 Answers
Q2.1 a. The target population is the adults in the Great Britain.
Q2.1 b. A sampling unit will be an adult in Great Britain. The article indicated that 12,000 British adults were sampled.
Q2.1 c. The variable being measured on each sampling unit will be e-cigarette use, with likely values ‘user’ or ‘not user’ (or ‘yes’ or ‘no’).
Q2.1 d. The population parameter will be the true number (or proportion) of e-cigarette users in Great British adults.
Q2.1 e. The sample estimate is the number (or proportion) of e-cigarette users in the sample of British adults.
Q2.2 It is likely that the people who phone in to the radio station hold strong feelings or opinions which may not reflect the opinions all those who listen or indeed of the general population.
Q2.3 a. Calculate the total population size \[ N = 7221 + 1763 + 1426 + 1174 = 11584\] The probability of an individual being selected is
\[ \frac{n}{N} = \frac{500}{11584} = 0.043\]
Each member of the university has a 0.043 chance of being selected in the sample.
Q2.3 b. For a systematic sample, the fixed periodic interval is given by
\[k = \frac{N}n = \frac{11584}{500} = 23.186 \sim 23\]
Q2.3 c. The first five elements of a systematic sample will be (\(q, q+k, q+2k, q+3k, q+4k)\). Thus, if \(k\)=23 and \(q=12\), the first five individuals selected will be (12, 35, 58, 81 and 104).
Q2.3 d. To calculate the sample size of each stratum, we first need to calculate the proportion of members in each strata. This is given by:
Undergraduates: \[\frac{7221}{11584} = 0.623 \]
Postgraduates: \[\frac{1763}{11584} = 0.152 \]
Academic and research staff: \[\frac{1426}{11584} = 0.123 \]
Support staff: \[\frac{1174}{11584} = 0.101 \]
Using these proportions, we can calculate the size of the sample in each group
Undergraduates: \[500 \times 0.623 = 311.68 \sim 312 \] individuals Postgraduates: \[500 \times 0.152 = 76.01 \sim 76 \] Academic and research staff: \[500 \times 123 = 61.56 \sim 62 \] Support staff: \[500 \times 0.101 = 50.67 \sim 51 \]
Note: this gives a total sample of 501 and so you can choose either to reduce one of the groups by one, or have a sample of 501 individuals.
Performing these calculations in R forms the basis of computer practical 2.
Q2.4 (Squire 1988) identified several problems which compounded the error in the result:
the sampling procedure was flawed - there were differences in voting patterns between those who received a questionnaire (i.e. those with car and/or a telephone) and those who did not receive a questionnaire,
a low response rate - although a large number of questionnaires were returned, this was still less than 25% of the total sent out,
non-response bias - those who returned their questionnaires favoured Landon. As an aside, George Gallup conducted a poll of 50,000 people and correctly predicted the result. Gallup remains a prominent election-polling organisation today.
Q2.5 a. This is a census of the imprisoned serial killer population and a sample (presumably not random) of the entire worldwide serial killer population.
Q2.5 b. Whilst the psychologist chose a random sample of serial killers, there may be a non-response bias in that only some chose to respond. These prisoners might have a different psychology compared to those that refused to participate.
There is another problem too; the imprisoned serial killers are a biased sample of the whole population of serial killers. Potential serial killers who are arrested after their first murder are not defined as serial killers and thus not included in the population. In addition, those not caught, presumably, could kill more than those who are imprisoned, thus, the mean number of victims could be under-estimated.
Q2.5 c. This is a stratified sampling scheme with country being the strata.
Q2.6 Yes. This question asks whether the drug works at all, so a control is required for comparison.
Q2.7 No. In this question, the drug is being compared to existing drugs so it is a contrast.
Q2.8 There is no definitive answer; one could argue that as the statistical ecologist did not create the conditions, it is an observational study.
Q2.9 It could be argued that because the industrialist deliberately manipulated the environment it is an experiment!
References
This is one definition of quasi-experiment, there are others↩︎