Chapter 8 Hypothesis Tests

The value for which \(P\)=0.05, or 1 in 20, is 1.96 or nearly 2; it is convenient to take this point as a limit in judging whether a deviation ought to be considered significant or not. Deviations exceeding twice the standard deviation are thus formally regarded as significant. Using this criterion we should be led to follow up a false indication only once in 22 trials, even if the statistics were the only guide available. Small effects will still escape notice if the data are insufficiently numerous to bring them out, but no lowering of the standard of significance would meet this difficulty.
R. A Fisher, 1971.

8.1 Introduction

A confidence interval provides a plausible range of values for an unknown parameter (e.g. the population mean). A hypothesis test is conducted to investigate a question e.g. does the application of fertilizer increase crop yield, does a new drug reduce blood pressure compared to a standard drug? These might be termed research hypotheses - the question that the study is designed to answer. In a one sample \(t\) test, a sample mean is compared to a known or hypothesised value. A two sample \(t\) test is used to determine if two population means are equal. In hypothesis testing, we try to determine the strength of evidence for a particular value given the data - this can be quantified by a probability, the \(p\)-value. Hypothesis tests such as \(t\) tests rely on assumptions but if these assumptions are not valid, alternative, non-parametric methods can be used.

This chapter describes

• the different types of hypotheses
• a one sample, two sample and paired \(t\) tests
• the differences between one- and two-tailed tests
• using a \(p\)-value or fixed significance level to make conclusions,
• non-parametric alternatives to \(t\) tests and
• statistical and practical significance.

8.1.1 Types of hypotheses

A study is generally designed with a research hypothesis in mind. To test a research hypothesis, two further hypotheses are required and these are defined with a specific format; a null hypothesis and an alternative hypothesis.

The null hypothesis (denoted by \(H_0\)) is the hypothesis that is tested and is very specific. In a one sample \(t\) test it specifies that there is no difference between the true mean (\(\mu\)) and the hypothesised value (say \(\mu_0\)). This is represented mathematically as:

\[H_0: \mu = \mu_0\] or equivalently,

\[H_0: \mu - \mu_0 = 0\] Example We wish to determine whether a sample of baby weights could have been generated from a population with a mean of 120 ounces; this is the research hypothesis to be tested. The null hypothesis would be

\[H_0: \mu = 120\]

The alternative hypothesis (denoted by \(H_1\) or \(H_A\)) could take several forms. Firstly, we could state that the true mean is not equal to the hypothesised value:

\[H_1: \mu \ne \mu_0\] This is called a two-tailed test because \(\mu\) could be either larger or smaller than \(\mu_0\) - the direction of any difference is not important. We could, however, be more precise and state a direction where we think the difference will lie, for example:

\[H_1: \mu < \mu_0\] or alternatively:

\[H_1: \mu > \mu_0\]

These are called one-tailed tests because the direction of the difference is important. For both one- and two-tailed tests, the null hypothesis will remain the same.

The alternative hypothesis for a two-tailed test of the birth weights will be:

\[H_1: \mu \ne 120\]

The example we have considered so far is a one sample test because we have one sample of data and we which to know whether it could have been generated from a process with a particular mean, e.g. 120 ounces.

We might be interested in determining whether data in two groups could have been generated from processes with the same or different means - this is a two sample test because we are comparing two samples, or groups. Assuming two groups, \(A\) and \(B\), the null hypothesis will be:

\[H_0: \mu_A = \mu_B\]

or

\[H_0: \mu_A - \mu_B = 0\]

Similar to a one sample test, the alternative hypotheses could be that the two means are not the same (two-tailed test):

\[H_1: \mu_A \ne \mu_B\]

or the means are different in some direction (one-tailed tests):

\[H_1: \mu_A < \mu_B\]

\[H_1: \mu_A > \mu_B\]

Having defined the test hypotheses, a test statistic is calculated and the strength of evidence for this statistic, assuming the null hypothesis is true, is quantified.

8.1.2 How do hypothesis tests work?

Hypothesis tests work by comparing an estimate obtained from the data (we call this a ‘data-estimate’) with what we expect to find assuming that \(H_0\) is true. The basic formulation of the test statistic (\(t_{stat}\)) is:

\[t_{stat}=\frac{\textrm{data-estimate - hypothesised value}}{\textrm{standard error of data-estimate}}\]

Evidence against the null hypothesis is provided by a large discrepancy between this data-estimate and the hypothesised value given by \(H_0\). If \(H_0\) is true, we expect the data-estimate and the hypothesised value to be similar and any difference is due to sampling variation alone.

However, detecting a difference from a particular value depends on the variability of the data and this is quantified by the standard error of the data-estimate. Consider a two sample test, where we want to decide whether any observed difference between the two group means is due to a real difference between the groups or whether it is due to sampling variability. Figure 8.1 illustrates two sets of data: group 1 has a mean of 30 and group 2 has a mean of 20; the standard deviation in the left hand panel is 2 for both groups and the standard deviation in the right hand panel is 8. A real difference between means seems:

• more compelling if the values within groups are tightly clustered (left-hand plot, Figure 8.1).

• less convincing if the values within each group are very variable (right-hand plot, Figure 8.1).

If there are no differences between group means (i.e. the null hypothesis is true) then any observed differences are likely to be small compared with the within-group variability (i.e. similar to the right-hand plot, Figure 8.1).

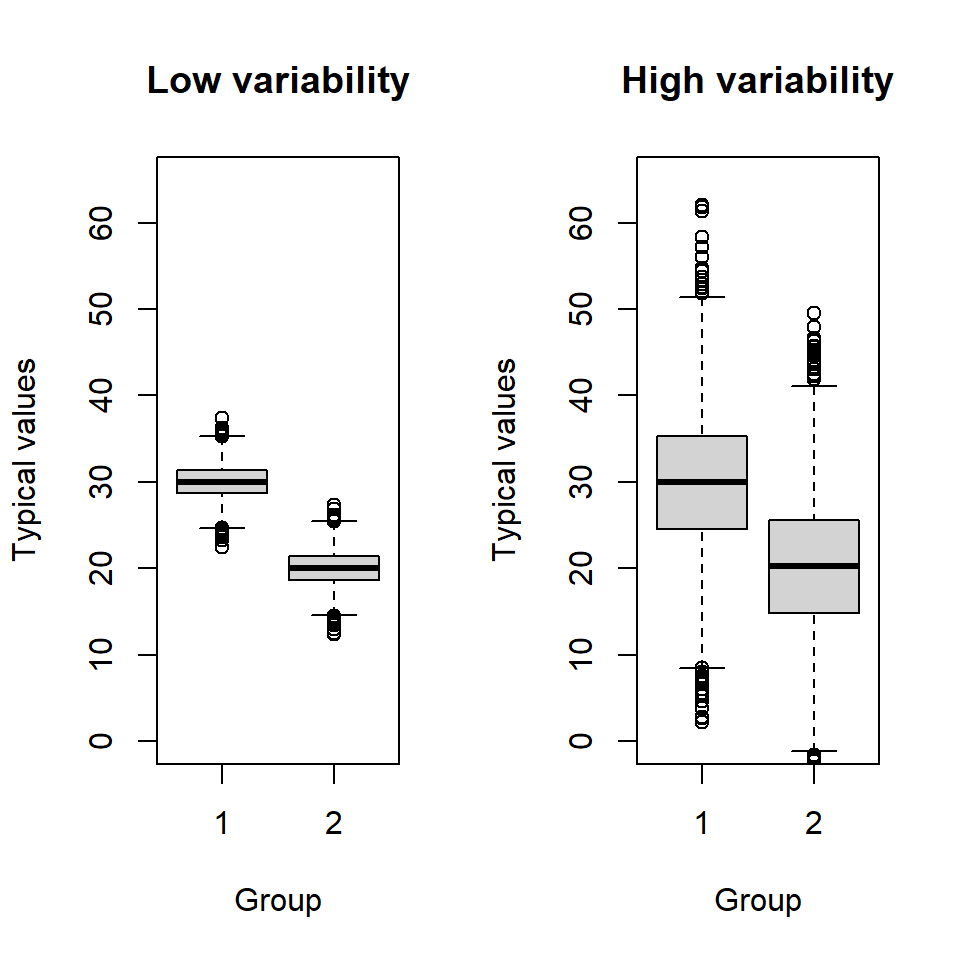
Figure 8.1: Box plots illustrating the distribution of data for two groups where the variability in the data is low (left) and high (right).

We use the ‘test statistic’ to quantify how much our data-estimate differs from the value in the null hypothesis taking into account the variability in the data. The formula for calculating the test statistic varies across data types and the nature of the test. In this chapter we consider one and two sample \(t\) tests to compare sample means; proportions are considered in a later chapter.

8.1.3 One sample \(t\) test

In a one sample \(t\) test we compare the data-estimate to the hypothesised value; the \(t\) test statistic is given by:

\[t_{stat}=\frac{\hat \mu - \mu_0}{se(\hat \mu)}\] where \(\hat \mu\) is the sample mean and \(se(\hat \mu)\) is the standard error of the sample mean.

Let’s return to the example where we want to determine whether the sample of baby weights could have been generated from a population with a mean of 120 ounces. As a reminder, the null hypothesis is:

\(H_0\): \({\mu} = 120\)

We will consider a two-tailed test and so the alternative hypothesis is:

\(H_1\): \({\mu} \neq 120\)

The sample statistics are: \(\hat\mu\)=119.5769, \(s\)=18.236 and \(n\)=1236. Substituting in these values we can calculate the standard error and test statistic.

The standard error is given by:

\[se(\hat\mu) = \frac{s}{\sqrt{n}} = \frac{18.24}{\sqrt{1236}} = 0.519\] The test statistic is, therefore,

\[t_{stat}=\frac{\hat{\mu} - 120}{se(\hat{\mu})} = \frac{119.577 - 120}{0.519} = -0.815\]

If \(H_0\) is true, the test statistic (\(t_{stat}\)) should be close to zero because the difference between the test statistic and the hypothesised value is small.

If \(H_0\) is false, the test statistic should be large (positive or negative) because the difference between the test statistic and the hypothesised value is large.

To decide if a test statistic is ‘large’ under the null hypothesis, we compare the test statistic to a reference distribution and, not surprisingly for a \(t\) test, we use the \(t\) distribution. The shape of the \(t\) distribution depends on the degrees of freedom and for a one sample \(t\) test the degrees of freedom (\(df\)) are given by \(df = n - 1\). Using this reference distribution we can determine what values might typically arise.

Having found the test statistic for the one sample test of baby weights, we obtain the associated reference \(t\) distribution. The sample size is 1236, and so \(df = 1236 - 1 = 1235\), hence, the reference distribution is a \(t_{df=1235}\) distribution (Figure 8.2). This figure shows that values close to zero are likely to occur and values smaller than -2, or greater than 2, are unlikely. Where the test statistic lies on the reference distribution indicates how typical it is given the null hypothesis.

The reference distribution can be used in two ways to determine the strength of evidence for the null hypothesis: by obtaining an exact \(p\)-value for the test statistic or using a pre-determined significance level.

8.1.3.1 Determining an exact \(p\)-value

A \(p\)-value is the probability of observing a test statistic at least as extreme as the one observed, given the null hypothesis is true. Thus,

• a test statistic close to zero would be likely to occur if was no difference between the data-estimate and the hypothesised value (other than sampling variability) and thus the probability of observing such a value would be high.

• a large, absolute value of the test statistic would be likely if there was a real difference between the data-estimate and the hypothesised value (over and above sampling variability) and thus the probability of observing such a value would be small.

A mathematical representation of the \(p\)-value for a two-tailed test is:

\[Pr(T \le -|t_{stat}|) + Pr(T \ge |t_{stat}|) \] where \(T\) is a random variable distributed as \(t_{df}\).

Using the \(t_{df=1235}\) distribution, the \(p\)-value associated with the test statistic of -0.815 can be obtained (Figure 8.2). We want the probability of a value smaller than -0.815 and the probability of a value greater than 0.815 (i.e. the areas in both tails of the distribution):

\[Pr(T \le -0.815) + Pr(T \ge 0.815) \]

The first part of this expression (i.e. \(Pr(T \le -0.815)\)) is the cumulative distribution function and because the distribution is symmetric we can easily find the value \(Pr(T \ge 0.815)\).

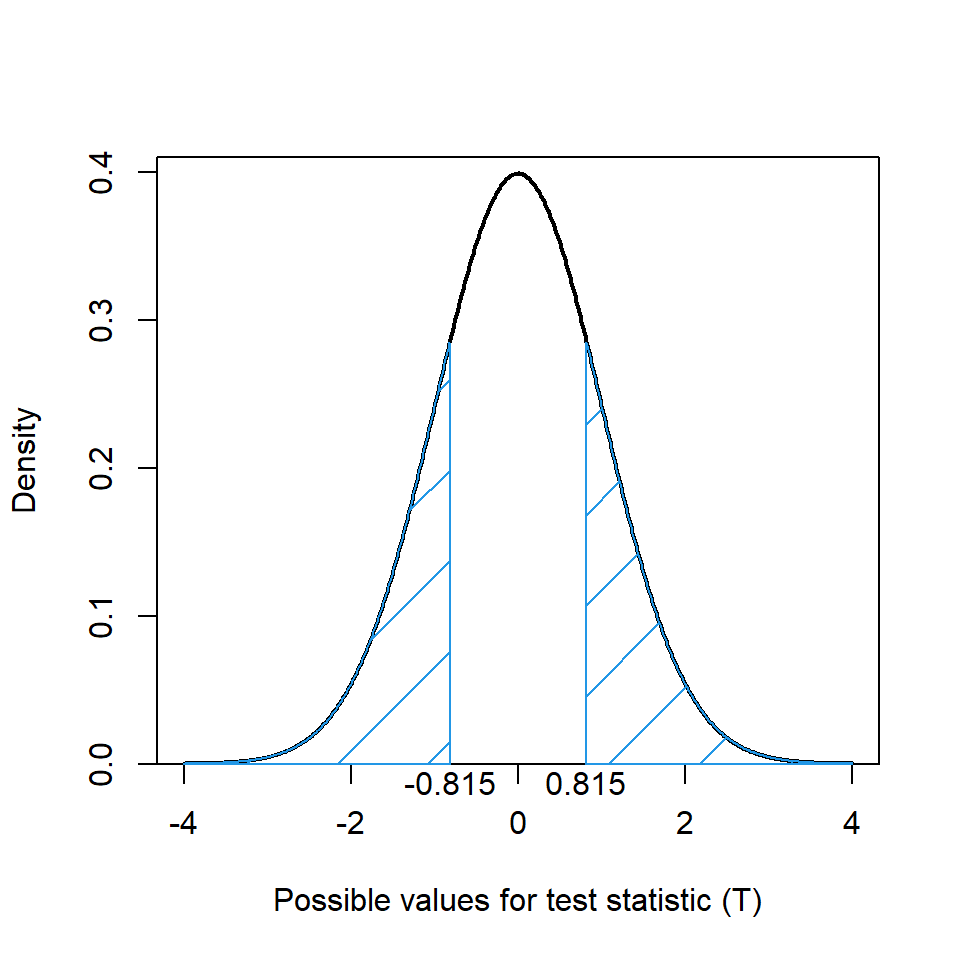
Figure 8.2: Reference \(t\) distribution for one sample example, \(t_{df=1235}\). The blue shaded region indicates areas more extreme than the test statistic (for a two-tailed test).

The blue shaded area on Figure 8.2 is a substantial proportion of the total area and is, in fact, 0.415 (= 0.2076 + 0.2076) of the area, hence the \(p\)-value is 0.415. What does this \(p\)-value indicate about how likely a test statistic of -0.815 is?

The \(p\)-value measures the strength of evidence against the null hypothesis and, typically, \(H_0\) is only rejected when the \(p\)-value is really small. What is classed as small? Common threshold values are 0.1, 0.05 or 0.01 and they can be translated as follows (Wild and Seber 1999):

Approximate \(p\)-value	Translation
>0.10	No evidence against \(H_0\)
0.05	Weak evidence against \(H_0\)
0.01	Strong evidence against \(H_0\)
\(\le\) 0.001	Very strong evidence against \(H_0\)

A \(p\)-value of 0.415 is pretty large, much larger than any of the values which provide evidence against \(H_0\) (shown in the table above). Hence, we conclude that the test statistic is consistent with \(H_0\); we are pretty likely to observe a test statistic of -0.815, or one more extreme. These data do not provide evidence to reject the null hypothesis and the sample of baby weights could come from an underlying population with a mean of 120 ounces.

Example The average age of the mothers in the sample (of size \(n=1236\)) from the US was 27.255 years with a standard deviation of 5.7814 years. The average age of first time mothers in the UK 2017 was 28.8 (The original data are here). Is there evidence to suggest that the age of mothers differ between the US and UK? We assume that the age of mothers in the UK was obtained from a census (and so there is no uncertainty).

The null hypothesis is:

\[H_0: \mu_{US} = 28.8\]

and since there is no reason to suspect that the average age in the US is either higher or lower than in the UK, we consider a two-tailed test and so the alternative hypothesis is:

\[H_1: \mu_{US} \ne 28.8\]

The standard error is given by:

\[se(\hat \mu_{US}) = \frac{s}{\sqrt{n}} = \frac{5.7814}{\sqrt{1236}} = 0.1644\]

and thus the test statistic is:

\[ t_{stat} = \frac{\hat \mu_{US} - 28.8}{se(\hat \mu_{US})} = \frac{27.255 - 28.8}{0.1664} = -9.285\]

We compare this to a reference distribution - since the sample size is 1236, the degrees of freedom for the reference distribution will be 1235. This is the distribution plotted in Figure 8.2 (since the sample size is the same as the sample of baby weights) and shows that a value of -9.285 will be out in the left hand tail (so much so that it is not even displayed on the \(x\)-axis scale.) In fact, the probability of obtaining a value as extreme, or more extreme, than -9.285 (i.e. \(Pr(T \le -0.9285)\)) is pretty much zero and even when added to the probability in right hand tail (i.e. \(Pr(T \ge 0.9285)\)) the \(p\)-value is approximately zero. Translating this value using the table above, there is strong evidence to reject \(H_0\) and conclude that the average age of the US mothers is not from a population with a mean of 28.8 years.

8.1.3.2 Using a fixed significance level

Some studies use a (pre-determined) fixed significance level; the evidence for the null hypothesis is determined with a 5% significance level, for example. We find a ‘critical value’ from the reference distribution based on the significance level and compare the test statistic to this critical value. Let’s return to the reference distribution for the baby weights and assume a fixed significance level of 5%; this is a two-tailed test (as specified in the alternative hypothesis) and so we want to find the quantile (the critical value, \(t_{crit}\)) such that:

\[Pr(T \le -|t_{crit}|) + Pr(T \ge |t_{crit}|) = 0.05\]

In Figure 8.3, the critical value, \(t_{crit}\) is 1.96 (i.e. the red shaded area is 5% of the total area) and we can see that the test statistic does not fall within the red shaded region. Hence, the conclusion is the same as before, there is no evidence to reject the null hypothesis, testing at a 5% significance level.

A test statistic falling within the red shaded region would be sufficiently unlikely (based on the significance level) to have occurred if the null hypothesis was true, hence, providing evidence to reject the null hypothesis.

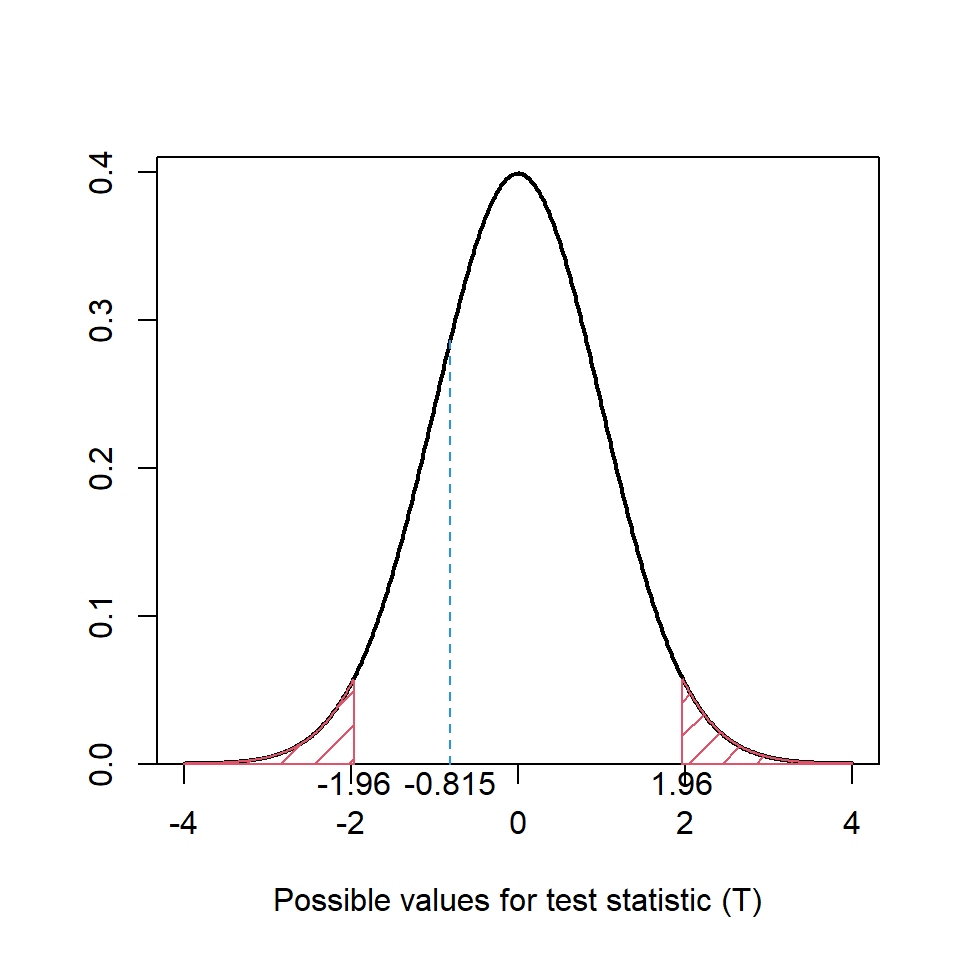
Figure 8.3: Reference \(t\) distribution for one sample example, \(t_{df=1235}\). The red shaded region indicates areas more extreme than the critical value. The blue dashed line indicates the test statistic.

This method of obtaining a critical value based on a fixed significance level and comparing it to the test statistic was used when making a decision regarding the null hypothesis was limited to looking up critical values in statistical tables. It is still frequently practised - it is commonplace to see the phrase ‘testing at a significance level of …’ in statistical reports. In more recent times, when access to computing power and statistical packages is commonplace, it is now easy to perform a test and obtain an exact \(p\)-value and indeed many computer packages routinely provide exact \(p\)-values in output.

8.1.3.3 Doing this in R

The function t.test was previously introduced to calculate a confidence interval; now we use it to perform a one sample \(t\) test on the baby weights. These data are stored in an object called baby and the weights are in a column called bwt. For a one sample test, the hypothesised value (mu) is specified and a two-tailed test (i.e. \(H_1: \mu \ne 120\)) is performed by default.

# One sample t test
t.test(x=baby$bwt, mu=120)

    One Sample t-test

data:  baby$bwt
t = -0.81574, df = 1235, p-value = 0.4148
alternative hypothesis: true mean is not equal to 120
95 percent confidence interval:
 118.5592 120.5945
sample estimates:
mean of x 
 119.5769 

The output provides information about the test; the test statistic, degrees of freedom and exact \(p\)-value, what alternative hypothesis has been specified, and the sample mean and 95% confidence interval for the sample mean.

The t.test function provides the \(p\)-value as part of the output, but we can also find this value from the pt function. In the command below, two alternative methods are used to find it.

# Finding the exact p-value
# 1. Calculate area in lower tail and multiply by 2
pt(q=-0.815, df=1235) * 2

[1] 0.4152294

# 2. Calculate area in both tails and add
pt(q=-0.815, df=1235) + pt(q=0.815, df=1235, lower.tail=FALSE)

[1] 0.4152294

The t.test function does not provide the critical value but this can be obtained from the qt function: for a two-tailed test, the significance level is distributed equally between the two tails. For a significance level of 5%, there will be 2.5% in each tail; by default, the area in the lower tail is provided.

# Left hand (lower) tail
qt(p=0.025, df=1235)

[1] -1.961887

# Right hand (upper) tail
qt(p=0.025, df=1235, lower.tail=FALSE)

[1] 1.961887

Q8.1 The weight of a chocolate bar was supposed to be 100 grams. To check the manufacturing process, a random sample of 100 bars were weighed; the sample mean was 99.06 grams and the standard deviation was 9.58.

a. State the null and alternative hypotheses to be tested with a two-tailed test.

b. Calculate a test statistic.

c. Based the following information, what do you conclude?

qt(p=0.025, df=99)

[1] -1.984217

d. What command would you use to calculate the exact \(p\)-value associated with the test statistic?

8.2 Two sample \(t\) test

In a two sample \(t\) test, we are interested in comparing means of continuous data from two groups (e.g. groups \(A\) and \(B\)). The test statistic is used to quantify the discrepancy between the data-estimate and the null hypothesis (i.e. no differences between the two means): \[H_0 : \mu_A = \mu_B\] or equivalently,

\[H_0 : \mu_A - \mu_B = 0\] The alternative hypothesis for a two-tailed test will be: \[H_1 : \mu_A - \mu_B \ne 0\]

The test statistic is given by:

\[t_{stat} = \frac{(\hat{\mu}_A - \hat{\mu}_B) - 0}{se(\hat{\mu}_A - \hat{\mu}_B)}\]

Example We continue to look at data collected from the observational study of birth weights introduced previously. We want to test whether babies born to mothers who did not smoke are heavier in weight compared to babies born to mothers who smoked. The summary data are provided in Table 8.1.

Table 8.1: Summary of birth weight data for the smoking and non-smoking groups (units are ounces).

Smoking	n	Mean	SD
No	742	123.05	17.4
Yes	484	114.11	18.1

We define the null hypothesis for the two groups, smokers (\(S\)) and non-smokers (\(N\)) as:

\[H_0: \mu_N - \mu_S = 0\]

The alternative hypothesis will be one-tailed because we want to see if babies in the non-smoking group are heavier than the smoking group babies.

\[H_1: \mu_N > \mu_S\] or

\[H_1: \mu_N - \mu_S > 0\]

Since we do not want to make the assumption that the standard deviations of the two groups are equal, we will calculate the standard error of the difference from:

\[se(\hat{\mu_N} - \hat{\mu_S})= \sqrt{\frac{{s_N}^2}{{n_N}} + \frac{{s_S}^2}{{n_S}}} = \sqrt{\frac{17.4^2}{742} + \frac{18.1^2}{484}} = 1.042\] Thus, the test statistic is:

\[t_{stat} = \frac{(123.05 - 114.11) - 0}{1.042} = 8.583\]

The degrees of freedom (for hand calculation) are given by finding the minimum value (\(Min\)) from the sample sizes for the two groups minus one:

\[df = Min(n_N-1, n_S-1) = Min(741, 483) = 483\]

Hence, the reference distribution is \(t_{df=483}\) and, because we are conducting a one-tail test, we are only interested in the probability associated with \(Pr(T \ge 8.583)\). Figure 8.4 shows that this probability is going to be very small because the test statistic is in the extreme right hand tail, i.e. the \(p\)-value is going to be close to zero. Hence, there is strong evidence to reject the null hypothesis and conclude that the babies from non-smoking mothers are heavier from smoking mothers.

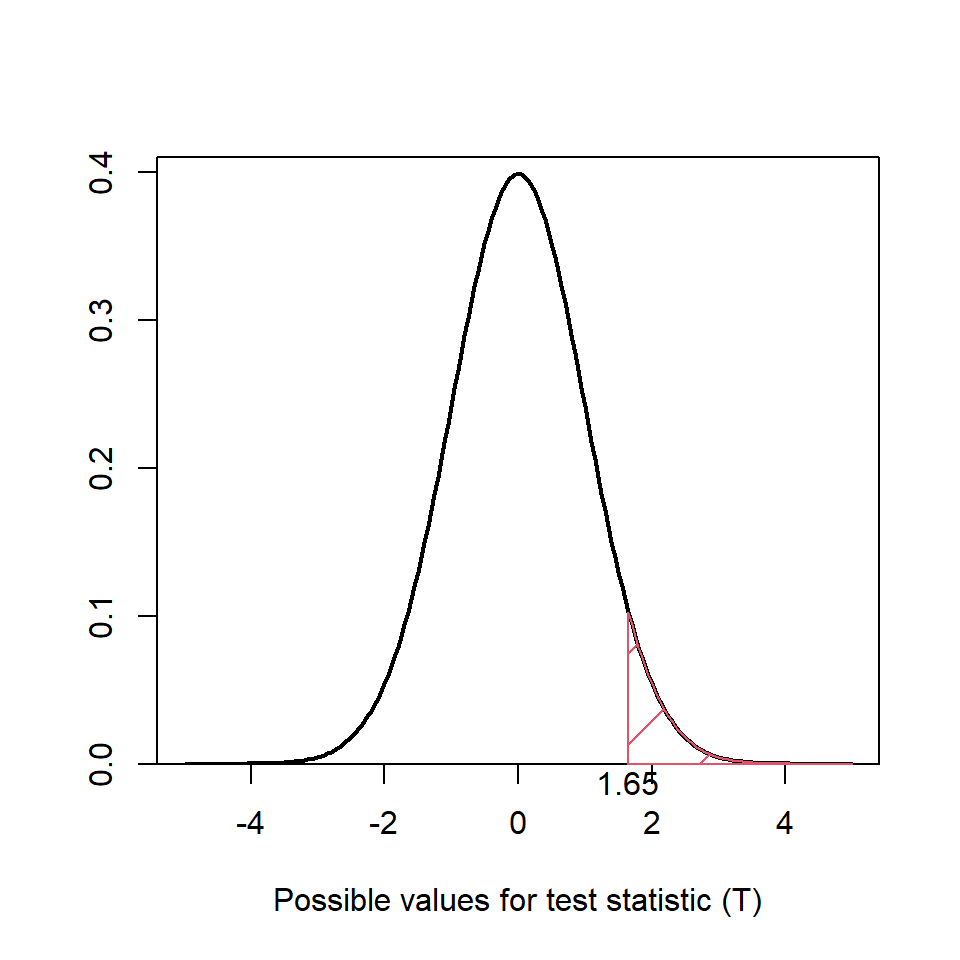
Figure 8.4: Reference \(t\) distribution for two sample test example, \(t_{df=483}\). The red shaded region indicates areas more extreme than the critical value for a one-tailed test.

To obtain the critical value associated with a significance level of 5%, we want the area in the right hand tail only - because this is a one-tailed test, i.e. \(Pr(T > t_{crit}) = 0.05\); this is the red shaded area in Figure 8.4. The test statistic is much larger than the critical value (\(t_{crit}=1.65\)) and thus there is evidence to suggest that the babies born to non-smoking mothers are heavier than babies born to mothers who smoked, testing at a 5% significance level.

8.2.1 Doing this in R

To make the code simple, separate objects are created for two groups. By default, a two-tailed test is performed but a one-tailed test can be specified using the alternative argument. Also by default, the standard deviations are assumed to be unequal and the degrees of freedom will be calculated using the Welch-Satterthwaite equation (Chapter 7).

# Save objects for two groups
grpN <- baby$bwt[baby$smoke==0]
grpS <- baby$bwt[baby$smoke==1]

# Two sample, one-tailed t test
t.test(x=grpN, y=grpS, alternative="greater")

    Welch Two Sample t-test

data:  grpN and grpS
t = 8.5813, df = 1003.2, p-value < 2.2e-16
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
 7.222928      Inf
sample estimates:
mean of x mean of y 
 123.0472  114.1095 

Since a one-tailed test has been specified, only one limit of the confidence interval for the difference in means is provided; in this example it is a plausible value for a lower limit i.e. that the weight of babies born to non-smoking mothers is likely to be at least 7.22 ounces.

The \(p\)-value in the output is found from:

# p-value in upper tail (using the Welch-Satterthwaite df)
pt(q=8.5813, df=1003.2, lower.tail=FALSE)

[1] 1.762554e-17

The critical value, testing at a significance level of 5% for a one-tailed test, would be found using the following command:

# Critical value (using df for hand calculation)
# Significance level is 5% for a one-tailed test
qt(p=0.05, df=482, lower.tail=FALSE)

[1] 1.648021

Q8.2 According to an advertising campaign, batteries from brand \(A\) last longer than batteries from brand \(B\). State the null and alternative hypotheses required to test this claim and hence, conduct a hypothesis test using the following data using a fixed significance level of 5%. Assume that the data are normally distributed. The following may be of use.

qt(p=0.05, df=59, lower.tail=FALSE)

[1] 1.671093

Brand	n	Mean	SD
A	90	49.5	6.32
B	60	46.1	3.31

Q8.3 An experiment looked at the effect of either a high or low protein diet on female rats. The gains in weight over a period of time were recorded and a two-sample \(t\) test was conducted; the R output is shown below.

    Welch Two Sample t-test

data:  hi.protein and lo.protein
t = 1.9107, df = 13.082, p-value = 0.07821
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -2.469073 40.469073
sample estimates:
mean of x mean of y 
      120       101 

a. State the null and alternative hypotheses that have been tested.

b. Given that the standard error for the difference in means used in this test was 9.944, explain how the test statistic was calculated.

c. Interpret the test results.

8.3 Paired \(t\) test

A paired \(t\) test is used to compare the population means of two groups where the observations in one sample can be paired with an observation in the other sample. An example would be a study where participants are measured before and after a treatment and so the two measurements are not independent since the measurements were taken from the same participants. These types of study can be very useful because using the same participants can eliminate any variation other than the treatment between the two groups.

Let \(x\) be a measurement before treatment, or some intervention, and \(y\) be a measurement after treatment. The difference between the two measurements on each participant \(i\) is given by:

\[d_i = x_i - y_i\]

The mean of the difference is calculated, here denoted by \(\bar d\), this essentially reduces the data to one sample; a paired \(t\) test is the same as a one sample \(t\) test on the differences. The null hypothesis is that the true mean of the differences is equal to zero:

\[H_0: \mu_d = 0\] The alternative hypothesis can be specified in several ways depending on whether a one or two-tailed test is required, for example:

\[H_1: \mu_d \ne 0\] \[H_1: \mu_d > 0\] \[H_1: \mu_d < 0\]

The test statistic is given by:

\[t_{stat} = \frac{\bar d - 0}{se(\bar d)} \]

The standard error of the differences is:

\[se(\bar d) = \frac{s_d}{\sqrt{n}}\] where \(s_d\) is the sample standard deviation of the differences.

Under the null hypothesis, the test statistic follows a \(t_{df=n-1}\) distribution and this can be used to obtain a \(p\)-value.

Example A study tested whether cholesterol level was reduced after using a certain brand of margarine as part of a low cholesterol diet. Eighteen participants incorporated the margarine into their daily diet and their cholesterol levels were measured at the start and after 4 and 8 weeks. Here we compare the cholesterol levels after 4 and 8 weeks (data can be found here). We do not make an assumption about whether cholesterol levels should be higher or lower after 8 weeks and hence use a two-tailed test.

The mean and standard deviation of the differences are \(\bar d = 0.0628\) and \(s_d = 0.0704\). The test statistic is then:

\[t_{stat} = \frac{0.0628}{\frac{0.0704}{\sqrt{18}}} = 3.78\] This is compared to a \(t_{df=17}\) distribution; Figure 8.5 shows that the test statistic lies in the right hand tail and so the probability of obtaining a value as extreme as this is going to be very small. The critical value is 2.11 and Figure 8.5 shows that the test statistic is much greater than the critical value. Therefore, there is some evidence to reject the null hypothesis and conclude that there is a difference in cholesterol levels between weeks 4 and 8.

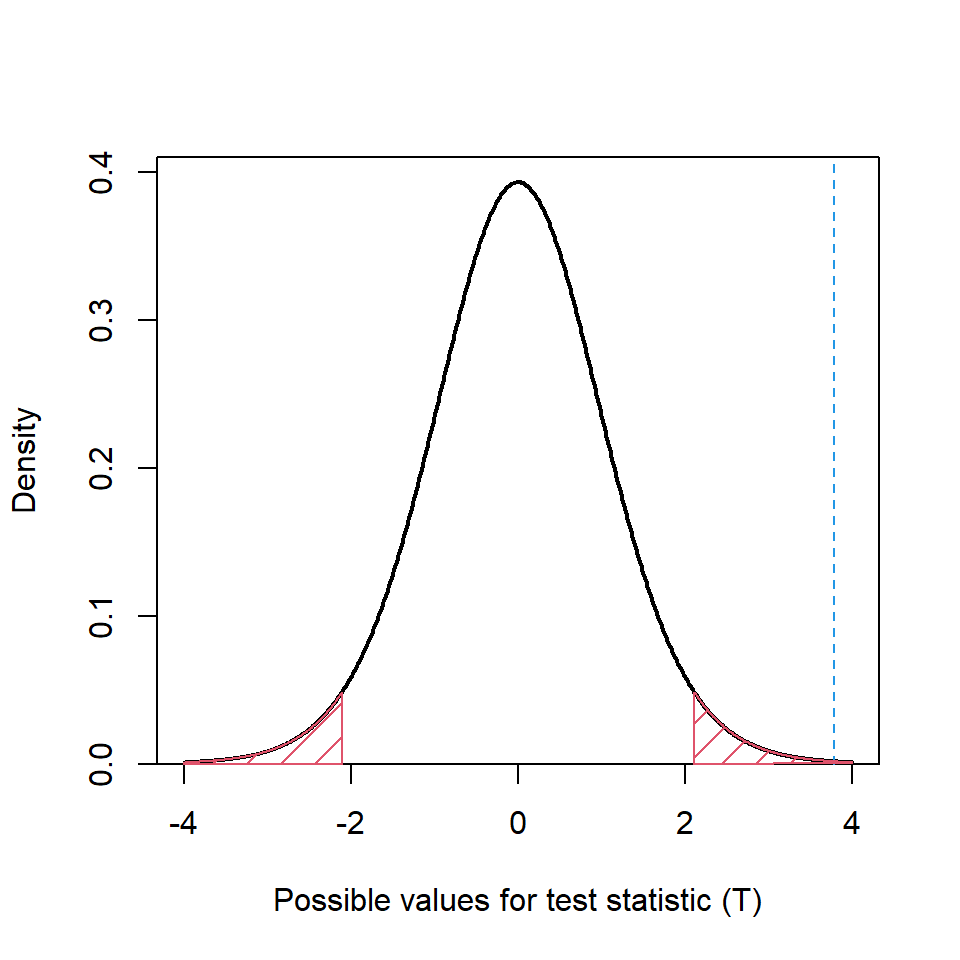
Figure 8.5: Reference \(t_{df}=17\) distribution for paired sample example. The blue dashed line indicates the test statistic and the red shaded region indicates areas more extreme than the critical value (testing at a significance level of 5%.

8.3.1 Doing this in R

The t.test function is used to perform a paired \(t\) test with an additional argument to indicate that the data are paired observations. In the example below, the cholesterol data have been stored in an object called chol.

# Paired t test
t.test(chol$After8weeks, chol$After4weeks, paired=TRUE)

    Paired t-test

data:  chol$After8weeks and chol$After4weeks
t = -3.7809, df = 17, p-value = 0.001491
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.09780897 -0.02774658
sample estimates:
mean of the differences 
            -0.06277778 

The similarity between this approach and using a one sample test of the differences is easily shown:

# Calculate the difference
diff <- chol$After8weeks - chol$After4weeks 

# One sample t test of differences
t.test(x=diff, mu=0)

    One Sample t-test

data:  diff
t = -3.7809, df = 17, p-value = 0.001491
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.09780897 -0.02774658
sample estimates:
  mean of x 
-0.06277778 

8.4 \(t\) test assumptions

Both one and two sample \(t\) tests are based on assumptions that need to be fulfilled for the results to be reliable. These assumptions are that the data are

1. independent (both within and between groups), and

2. normally distributed.

The first assumption can be determined by having knowledge of the data collection procedures and what the data represent. If the sampling units in the groups are paired, then a paired \(t\) test can be undertaken.

The second assumption can be checked by plotting the data, for example using histograms and boxplots. This will be explored further in the chapter 9.

If the data are not normally distributed, then a non-parametric test can be used and so we look at this next.

Q8.4 For the test described in Q8.3, as well as an assumption regarding standard deviations of the two groups, state two other assumptions on which this test was based.

8.5 Non-parametric alternative to \(t\) tests

The \(t\) test assumes that the data are normally distributed and, although the test is quite robust if data are not exactly normally distributed (i.e. the test result is still valid), in some situations the data will be skewed or the sample size will be small. In these circumstances, non-parametric, or distribution-free, methods are available. However, these methods still assume that the data are independent within and between groups.

To determine if two data samples have the same population mean, the Mann-Whitney-Wilcoxon test is used.

8.5.1 Mann-Whitney-Wilcoxon test

This test is known by various names (e.g. Mann-Whitney, two-sample Wilcoxon). The null hypothesis is that the two groups (say \(A\) and \(B\)) have the same distributions - represented as \(H_0: A = B\). The alternative hypothesis is that there is a shift in the distribution; if there is no reason to suggest a shift to the left or right, the alternative hypothesis will \(H_1: A \ne B\). One-tailed variants (i.e. \(H_1: A < B\) or \(H_1: A > B\)) can also be tested.

Example To illustrate the test procedure, six baby weights from the smoking group and six from the non-smoking group are used. The data in the two groups are

Non-smoking (N): 120, 113, 123, 136, 138, 132

Smoking (S): 128, 108, 143, 144, 141, 110

The test statistic is based on sorting the data into order and assigning ranks - the ranks in each group are then added together. The procedure is:

1. Combine the values (weights) from both groups and rank them in order of increasing value.

Weight	Group	Rank
108	S	1
110	S	2
113	N	3
120	N	4
123	N	5
128	S	6
132	N	7
136	N	8
138	N	9
141	S	10
143	S	11
144	S	12

2. Calculate the sum of ranks for each group:

\[R_N = 3 + 4 + 5 + 7 + 8 + 9 = 36\] \[R_S = 1 + 2 + 6 + 10 + 11 + 12 = 42\]

3. Calculate a test statistic for both groups:

\[W_N = R_N - \frac{n_N(n_N + 1)}{2} = 36 - \frac{6 \times 7}{2} = 15\]

\[W_S = R_S - \frac{n_S(n_S + 1)}{2} = 42 - \frac{6 \times 7}{2} = 21\]

4. Either of these values are used as the test statistic - the smaller value is generally used when consulting statistical tables to determine a critical value (There are some statistical tables here) and then the test statistic would be compared to the critical value as described previously. Here, we use R and R uses the test statistic for the first group specified in the command (see below).

There are also one sample and paired sample variants of the Mann-Whitney-Wilcoxon test and these are illustrated below.

8.5.1.1 Doing this in R

The function is called wilcox.test and, as in the example above, only the first six weights in each group are used.

wilcox.test(x=grpN[1:6], y=grpS[1:6])

    Wilcoxon rank sum exact test

data:  grpN[1:6] and grpS[1:6]
W = 15, p-value = 0.6991
alternative hypothesis: true location shift is not equal to 0

The \(p\)-value is interpreted as before; here it is large and thus provides no evidence to reject the null hypothesis.

For large samples, the test statistic \(W\) is approximately normally distributed and so the \(p\)-value is obtained from the normal distribution and a correction is applied to account for this approximation: we can see this using all the data for the baby weights.

wilcox.test(x=grpN, y=grpS)

    Wilcoxon rank sum test with continuity correction

data:  grpN and grpS
W = 231918, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0

A one sample version is available; here the null hypothesis can be interpreted as the median is equal to some hypothesised value:

\[H_0: \textrm{median} = \textrm{median}_0\]

To illustrate the command for the baby weights:

wilcox.test(x=baby$bwt, mu=120)

    Wilcoxon signed rank test with continuity correction

data:  baby$bwt
V = 358753, p-value = 0.7062
alternative hypothesis: true location is not equal to 120

To illustrate a paired sample variant of the Mann-Whitney-Wilcoxon test, we return to the cholesterol data.

# Paired sample
wilcox.test(x=chol$After4weeks, y=chol$After8weeks, paired=TRUE)

    Wilcoxon signed rank test with continuity correction

data:  chol$After4weeks and chol$After8weeks
V = 152.5, p-value = 0.003725
alternative hypothesis: true location shift is not equal to 0

8.6 Practical significance versus statistical significance

The word ‘significant’ can often cause confusion - in hypothesis tests a significant result frequently means the \(p\)-value is less than 0.05. It does not necessarily imply that the result (for example, a difference between means) is substantial and has practical significance. Indeed we sometimes define the significance as part of our test e.g. 0.05, and another analysis might use a different value to determine significance. To illustrate the practical significance, confidence intervals should be reported along with the test results.

Statistical significance:

• relates to the existence of an effect,

• it can be found with small differences if the sample size is large enough (because the standard error will be small).

Practical (or clinical) significance:

• relates to the size of an effect and should be reported to provide context to the hypothesis test results.

For an interesting (and short) read about practical and statistical significance have a look at this Significance Magazine article.

8.7 Summary

This chapter has covered the underlying concepts of hypothesis testing; a test statistic is obtained and compared to a reference distribution. Where the test statistic lies on this reference distribution provides evidence to either reject, or not reject, the null hypothesis. In terms of the \(p\)-value:

• a small \(p\)-value indicates that the test statistic is very unlikely to be obtained when the null hypothesis is true - \(H_0\) is rejected in favour of \(H_1\).

• a large \(p\)-value indicates the test statistic is likely to be obtained when the null hypothesis is true - \(H_0\) cannot be rejected.

The \(t\) tests rely on data being normally distributed; if this is not a valid assumption, non-parametric tests can be used.

In chapter 9, we consider hypothesis tests for when there are more than two groups. For more information about hypothesis testing in general see.

8.7.1 Learning outcomes

In this chapter you have seen how to

1. define test hypotheses and determine whether one-tailed or two-tailed tests should be used,

2. calculate a test statistic for a one, two and paired sample \(t\) tests,

3. decide whether to reject, or otherwise, the null hypothesis based on the \(p\)-value and testing at a fixed significance level,

4. use a non-parametric alternative to \(t\)-tests, and

5. consider the practical and statistical significance of a test.

8.8 Answers

Q8.1 The sample statistics were \(n\)=100, \(\hat \mu = 99.06\) and \(s=9.58\).

Q8.1 a. We want to determine if the population mean could be 100 grams. The null and alternative hypotheses to be tested with a two-tailed test are:

\[H_0: \mu = 100\]

\[H_1: \mu \ne 100\]

Q8.1 b. The test statistic is

\[t_{stat} = \frac{\hat \mu - m_0}{\frac{s}{\sqrt{n}}} = \frac{99.06 - 100}{\frac{9.58}{\sqrt{100}}} = -0.9812\]

Q8.1 c. The value provided in the output (i.e. -1.984) was the critical value (\(t{crit}\)) in the lower tail, testing at a fixed significance level of 5%. In this case \(t_{crit} < t_{stat}\) and so there is no evidence to reject the null hypothesis; the sample could have been generated from a population with mean 100 grams.

d. The exact \(p\)-value associated with the test statistic for a two-tailed test will be provided by the command:

pt(q=-0.9812, df=99) * 2

[1] 0.3288859

Q8.2 The claim is that Brand A batteries last longer than Brand B. Therefore, the hypotheses will be:

\[H_0: \mu_A - \mu_B = 0\]

\[H_1: \mu_A - \mu_B > 0\]

The test statistic is given by

\[t_{stat} = \frac{(\hat \mu_A - \hat \mu_B) - 0}{se(\mu_A - \hat \mu_B)}\]

First calculate the standard error of the difference:

\[se(\hat{\mu_A} - \hat{\mu_B})= \sqrt{\frac{{s_A}^2}{{n_A}} + \frac{{s_B}^2}{{n_B}}} = \sqrt{\frac{6.32^2}{90} + \frac{3.31^2}{60}} = 0.7915\] Thus, the test statistic is:

\[t_{stat} = \frac{(49.5 - 46.1) - 0}{0.7915} = 4.2956\]

For ease of calculation, the degrees of freedom for the relevant \(t\) distribution are given by:

\[df = Min(n_A - 1, n_B - 1) = Min(89, 59) = 59\]

The critical value will be found from R and since this is a one-tailed test, we only want the area in the upper tail.

qt(p=0.05, df=59, lower.tail=FALSE)

[1] 1.671093

This value is less than the test statistic and so there is evidence to reject the null hypothesis, testing at a 5% significance level, and conclude that brand A lasts longer than brand B.

The exact \(p\)-value is found using the pt function:

pt(q=4.2956, df=59, lower.tail=FALSE)

[1] 3.298826e-05

In confirmation, the \(p\)-value is small (i.e. <0.001).

Q8.3 Let the two groups, high protein and low protein diets, be defined by \(H\) and \(L\), respectively.

Q8.3 a. The null and alternative hypotheses are

\[H_0: \mu_H - \mu_L = 0\] \[H_1: \mu_H - \mu_L \ne 0\]

Q8.3 b. The test statistic was calculated from the data estimate (difference in means) minus the hypothesised value divided by the standard error of the difference.

\[\textrm{test statistic} = \frac{(\hat \mu_H - \hat \mu_L) - 0}{se(\hat \mu_H - \hat \mu_L)}\]

\[ 1.9107 =\frac{120 - 101}{9.944} \] Q8.3 c. The \(p\)-value is 0.07821 which provides weak evidence to reject the null hypothesis.

Q8.4 The two remaining assumptions are:

1. Independence of the data within and between groups.

2. Data are normally distributed.

References

Wild, C. J., and G. A. F. Seber. 1999. Chance Encounters: A First Course in Data Analysis and Inference. Wiley.